§2  线性空间与线性子空间

一、线性空间

[线性运算]   设F是一个域，其元素a，b，c，…作为数量；V是任一种类对象的集，其元素用希腊字母α,β,γ,…表示. 确定两个运算法则：
    1^o  V中元素的加法.  对V中任二元素α，β，总有唯一确定的元素γ与它们对应，称为α与β之和，记作.
    2^o F中的数量与V中元素的乘法.  对F中任一数a与V中任一元α，总有唯一确定的元素δ与它们对应，称为a与α的数乘，记作

 这两个运算法则称为线性运算.
    [线性空间及其性质]   设F是一个域，V是任一种类对象的集，若对线性运算满足以下条件，则称V为域F上的线性空间：
    (i)  V是一个加法群；
    (ii)  对任意元a∈F与α∈V，对应着唯一确定的一个元
    (iii) 满足分配律和结合律，即对有               

域F的元素称为线性空间的数量，V的元素称为它的矢量，因而线性空间又称矢量空间. 加法群的单位元称为零矢量，记作0，（-1）α是α∈V的逆元，称为负矢量.
    实数域上的线性空间称为实线性空间；复数域上的线性空间称为复线性空间.

    例1  三维空间中的矢量全体组成一个实线性空间.

    例2  数域F上的多项式环F[x]，按照通常的多项式加法与多项式乘法，组成数域F上的线性空间.

    例3  元素属于数域F的m×n矩阵，按照矩阵的加法和矩阵与数的乘法，组成数域F上的线性空间.

    例4  按照通常的加法和乘法，实数全体是实数域R上的线性空间. 复数全体是复数域C上的线性空间. 任一域是用自己当作数量域的线性空间.

    例5  把在一个实区间（a，b）中定义的每个连续实函数当作一个元素，任意两个元素f与g的和记作，是在中定义的一个连续实函数，它在每一点x的值规定为

又把一个元素f乘实数c所得到的元素规定为

则这些元素全体组成一个实线性空间.

线性空间有以下性质：

1^o零矢量是唯一的.

2^o负矢量是唯一的.

3^o.

4^o若则c=0或α=0.

[线性相关与线性无关]  域F上的线性空间V中一组有限个矢量,如果对,仅当时等式

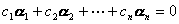
才成立，则称矢量组为线性无关，否则称为线性相关. 若矢量组线性相关，则其中至少有一个矢量是其余矢量的一个线性组合：

    含零矢量0的任一组矢量是线性相关的.
    假定域F上的线性空间V上又定义了收敛性（第二十一章，§3，四）,V中一组无限多个矢量,如果对F中的仅当时等式
                           
才成立，则称矢量为线性无关，否则称为线性相关.

    [基底与坐标]  域F上的线性空间V中一组矢量如果满足

    (i) 是线性无关的;

    (ii) V中任一矢量都是矢量的一个有限线性组合；则称为V的一个有限基底，也称生成（或张成）这个空间，为空间的一组生成元.

设为V的一组基底，则V中任一矢量α一定可以用的线性组合来表示：

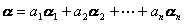
式中复数是唯一确定的，它称为矢量α关于基底的坐标.

如果V有一个有限基底，就称V是一个有限维线性空间，否则，称为无限维空间. 有限维线性空间V的基底的矢量个数称为V的维数，记作.

    [第一维数定理]  域F上有限维线性空间V的任意两个基底有相同个数的元素.

    推论  设为一个n维线性空间V中一组线性无关的矢量，显然，则在V中存在一个基底使得是它的一部分.