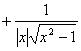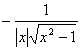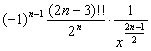3.函数的微分与高阶导数
[函数的微分] 若函数y=f(x)的改变量可表为
＝A(x)dx+o(dx)
式中dx=Δx，则此改变量的线性主部A(x)dx称为函数y的微分,记作
dy=A(x)dx
函数y=f(x)的微分存在的充分必要条件是:函数存在有限的导数
=
,这时函数的微分是
dy=
dx
上式具有一阶微分的不变性,即当自变量x又是另一自变量t的函数时,上面的公式仍然成立.
[高阶导数] 函数y=f(x)的高阶导数由下列关系式逐次地定义出来(假设对应的运算都有意义)：
=
[高阶微分] 函数y=f(x)的高阶微分由下列公式逐次定义：
=
式中
.并且有
=
及
[莱布尼茨公式] 若函数u=
及
=
有n阶导数(可微分n次),则
式中
,
,
为二项式系数。
同样有
式中
，
更一般地有
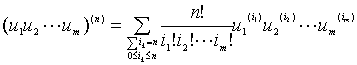
式中m，n为正整数。
[复合函数的高阶导数] 若函数y=f(u),u=
有l阶导数，则
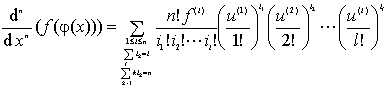
式中
，
[基本函数的导数表]
|
f(x) |
|
f(x) |
|
|
c |
0 |
|
|
|
xn |
nxn－1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh x |
chx |
|
|
|
ch x |
shx |
|
|
|
th x |
|
|
|
|
cth x |
|
|
|
|
sech x |
|
|
|
|
csch x |
|
|
|
|
|
|
|
|
|
Ar sech x |
f>0取 |
|
|
|
Ar csch x |
|
Arch x=
|
f>0取+，f<0 |
|
|
Arth x=
(｜x｜<1) |
|
ln ch x |
th x |
|
Arcthx=
(｜x｜>1) |
|
ln |
|
,x>0
,x>1
[简单函数的高阶导数表]
|
f(x) |
|
|
|
m(m－1)…(m－n+1) |
|
|
这里(2n+1)!!=(2n+1)(2n－1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
shx |
shx(n为偶数)，chx(n为奇数) |
|
chx |
chx(n为偶数)，shx(n为奇数) |
(
=0)
