Given a homogeneous linear Second-Order Ordinary Differential Equation,
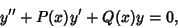 |
(1) |
call the two linearly independent solutions 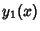 and
and 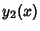 . Then
. Then
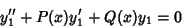 |
(2) |
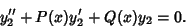 |
(3) |
Now, take 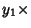 (3) minus
(3) minus 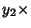 (2),
(2),
![\begin{displaymath}
y_1[y''_2+P(x)y'_2+Q(x)y_2]-y_2[y''_1+P(x)y'_1+Q(x)y_1]=0
\end{displaymath}](a_55.gif) |
(4) |
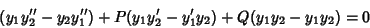 |
(5) |
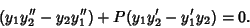 |
(6) |
Now, use the definition of the Wronskian and take its Derivative,
Plugging  and
and 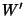 into (6) gives
into (6) gives
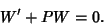 |
(9) |
This can be rearranged to yield
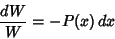 |
(10) |
which can then be directly integrated to
![\begin{displaymath}
\ln\left[{W(x)\over W_0}\right]= - \int P(x)\,dx,
\end{displaymath}](a_68.gif) |
(11) |
where 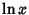 is the Natural Logarithm. Exponentiation then yields Abel's identity
is the Natural Logarithm. Exponentiation then yields Abel's identity
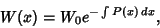 |
(12) |
where 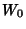 is a constant of integration.
is a constant of integration.
See also Ordinary Differential Equation--Second-Order
References
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed.
New York: Wiley, pp. 118, 262, 277, and 355, 1986.
© 1996-9 Eric W. Weisstein
1999-05-25