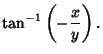A Map Projection. The inverse equations for  are computed by iteration.
Let the Angle of the projection plane be
are computed by iteration.
Let the Angle of the projection plane be 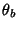 . Define
. Define
![\begin{displaymath}
a=\cases{
0 & for $\theta_b={\textstyle{1\over 2}}\pi$\cr
...
...ver 2}}({\textstyle{1\over 2}}\pi-\theta_b)]} & otherwise.\cr}
\end{displaymath}](a_526.gif) |
(1) |
For proper convergence, let 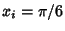 and compute the initial point by checking
and compute the initial point by checking
![\begin{displaymath}
x_i=\left\vert{\mathop{\rm exp}\nolimits [-(\sqrt{x^2 + y^2} + a\tan x_i)\tan x_i]}\right\vert.
\end{displaymath}](a_528.gif) |
(2) |
As long as 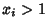 , take
, take 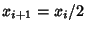 and iterate again. The first value for which
and iterate again. The first value for which 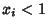 is then the starting point.
Then compute
is then the starting point.
Then compute
![\begin{displaymath}
x_i=\cos^{-1}\{\mathop{\rm exp}\nolimits [-(\sqrt{x^2+y^2} + a\tan x_i)\tan x_i]\}
\end{displaymath}](a_532.gif) |
(3) |
until the change in 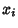 between evaluations is smaller than the acceptable tolerance. The (inverse) equations are then
given by
between evaluations is smaller than the acceptable tolerance. The (inverse) equations are then
given by
© 1996-9 Eric W. Weisstein
1999-05-25
![]() are computed by iteration.
Let the Angle of the projection plane be
are computed by iteration.
Let the Angle of the projection plane be ![]() . Define
. Define
![\begin{displaymath}
a=\cases{
0 & for $\theta_b={\textstyle{1\over 2}}\pi$\cr
...
...ver 2}}({\textstyle{1\over 2}}\pi-\theta_b)]} & otherwise.\cr}
\end{displaymath}](a_526.gif)