|
|
|
Consider the probability ![]() that no two people out of a group of
that no two people out of a group of ![]() will have matching birthdays out of
will have matching birthdays out of ![]() equally possible birthdays. Start with an arbitrary person's birthday, then note that the probability that the second person's
birthday is different is
equally possible birthdays. Start with an arbitrary person's birthday, then note that the probability that the second person's
birthday is different is ![]() , that the third person's birthday is different from the first two is
, that the third person's birthday is different from the first two is
![]() ,
and so on, up through the
,
and so on, up through the ![]() th person. Explicitly,
th person. Explicitly,
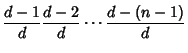 |
|||
![$\displaystyle {(d-1)(d-2)\cdots[d-(n-1)]\over d^{n-1}}.$](b_1523.gif) |
(1) |
| (2) |
| (3) |
| (4) |
The probability ![]() can be estimated as
can be estimated as
| (5) | |||
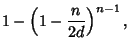 |
(6) |
| (7) |
In general, let ![]() denote the probability that a birthday is shared by exactly
denote the probability that a birthday is shared by exactly ![]() (and no more) people out of a group of
(and no more) people out of a group of
![]() people. Then the probability that a birthday is shared by
people. Then the probability that a birthday is shared by ![]() or more people is given by
or more people is given by
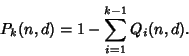 |
(8) |
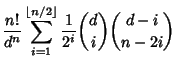 |
|||
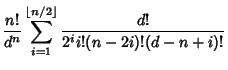 |
|||
![$\displaystyle {(-1)^n\over d^n}\left[{2^{-n/2}\Gamma(1+n)P_n^{(-d)}({\textstyle{1\over 2}}\sqrt{2})-{\Gamma(1+d)\over\Gamma(1+d-n)}}\right],$](b_1546.gif) |
(9) |
where ![]() is a Binomial Coefficient,
is a Binomial Coefficient, ![]() is a Gamma Function, and
is a Gamma Function, and
![]() is an
Ultraspherical Polynomial. This gives the explicit formula for
is an
Ultraspherical Polynomial. This gives the explicit formula for ![]() as
as
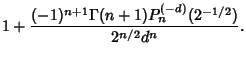 |
(10) |
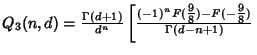
|
|
![$ \left.{+(-1)^n\Gamma(1+n)\sum_{i=1}^{\left\lfloor{n/3}\right\rfloor } {(-3)^{-...
...(i-d)}({\textstyle{1\over 2}}\sqrt{2}\,)\over\Gamma(d-i+1)\Gamma(i+1)}}\right],$](b_1555.gif)
|
|
|
|
(11) |
![$F=F(n,d,a)\equiv 1-{}_3F_2\left[{\!\!\matrix{{\textstyle{1\over 3}}(1-n), {\tex...
...\cr {\textstyle{1\over 2}}(d-n+1), {\textstyle{1\over 2}}(d-n+2)\cr}; a}\right]$](b_1556.gif)
|
|
|
|
(12) |
In general, ![]() can be computed using the Recurrence Relation
can be computed using the Recurrence Relation
![\begin{displaymath}
Q_k(n,d)=\sum_{i=1}^{\left\lfloor{n/k}\right\rfloor } \left[...
...m_{j=1}^{k-1} Q_j(n-k,d-i){(d-i)^{n-ik}\over d^{n-ik}}}\right]
\end{displaymath}](b_1559.gif) |
(13) |
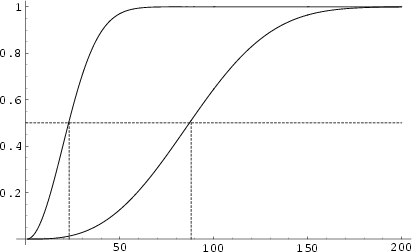
A good approximation to the number of people ![]() such that
such that ![]() is some given value can be given by solving the equation
is some given value can be given by solving the equation
| (14) |
| (15) |
The ``almost'' birthday problem, which asks the number of people needed such that two have a birthday within a day of each other,
was considered by Abramson and Moser (1970), who showed that 14 people suffice. An approximation for the minimum number of
people needed to get a 50-50 chance that two have a match within ![]() days out of
days out of ![]() possible is given by
possible is given by
| (16) |
See also Birthday Attack, Coincidence, Small World Problem
References
Abramson, M. and Moser, W. O. J. ``More Birthday Surprises.'' Amer. Math. Monthly 77, 856-858, 1970.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 45-46, 1987.
Bloom, D. M. ``A Birthday Problem.'' Amer. Math. Monthly 80, 1141-1142, 1973.
Bogomolny, A. ``Coincidence.''
http://www.cut-the-knot.com/do_you_know/coincidence.html.
Clevenson, M. L. and Watkins, W. ``Majorization and the Birthday Inequality.'' Math. Mag. 64, 183-188, 1991.
Diaconis, P. and Mosteller, F. ``Methods of Studying Coincidences.'' J. Amer. Statist. Assoc. 84, 853-861, 1989.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 31-32, 1968.
Finch, S. ``Puzzle #28 [June 1997]: Coincident Birthdays.''
http://www.mathsoft.com/mathcad/library/puzzle/soln28/soln28.html.
Gehan, E. A. ``Note on the `Birthday Problem.''' Amer. Stat. 22, 28, Apr. 1968.
Heuer, G. A. ``Estimation in a Certain Probability Problem.'' Amer. Math. Monthly 66, 704-706, 1959.
Hocking, R. L. and Schwertman, N. C. ``An Extension of the Birthday Problem to Exactly
Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 102-103, 1975.
Klamkin, M. S. and Newman, D. J. ``Extensions of the Birthday Surprise.'' J. Combin. Th. 3, 279-282, 1967.
Levin, B. ``A Representation for Multinomial Cumulative Distribution Functions.'' Ann. Statistics 9, 1123-1126, 1981.
McKinney, E. H. ``Generalized Birthday Problem.'' Amer. Math. Monthly 73, 385-387, 1966.
Mises, R. von. ``Über Aufteilungs--und Besetzungs-Wahrscheinlichkeiten.'' Revue de la Faculté des Sciences de l'Université
d'Istanbul, N. S. 4, 145-163, 1939. Reprinted in Selected Papers of Richard von Mises, Vol. 2 (Ed. P. Frank,
S. Goldstein, M. Kac, W. Prager, G. Szegö, and G. Birkhoff). Providence, RI: Amer. Math. Soc., pp. 313-334, 1964.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 179-180,
1994.
Sayrafiezadeh, M. ``The Birthday Problem Revisited.'' Math. Mag. 67, 220-223, 1994.
Sevast'yanov, B. A. ``Poisson Limit Law for a Scheme of Sums of Dependent Random Variables.'' Th. Prob. Appl. 17, 695-699, 1972.
Sloane, N. J. A.
A014088 and
A033810
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Stewart, I. ``What a Coincidence!'' Sci. Amer. 278, 95-96, June 1998.
Tesler, L. ``Not a Coincidence!'' http://www.nomodes.com/coincidence.html.
![]() Matches.'' College Math. J. 17,
315-321, 1986.
Matches.'' College Math. J. 17,
315-321, 1986.
|
|
|
© 1996-9 Eric W. Weisstein