Bloch Constant

N.B. A detailed on-line essay by S. Finch was the starting point for this entry.

Let $F$ be the set of Complex analytic functions $f$ defined on an open region containing the closure of the unit disk $D=\{z: \vert z\vert<1\}$ satisfying $f(0)=0$ and $df/dz(0)=1$. For each $f$ in $F$, let $b(f)$ be the Supremum of all numbers $r$ such that there is a disk $S$ in $D$ on which $f$ is One-to-One and such that $f(S)$ contains a disk of radius $r$. In 1925, Bloch (Conway 1978) showed that $b(f)\geq 1/72$. Define Bloch's constant by

$$B\equiv\inf\{b(f): f\in F\}.$$

Ahlfors and Grunsky (1937) derived

$$0.433012701\ldots = {\textstyle{1\over 4}}\sqrt{3} \leq B < ... ...11\over 12}})\over\Gamma({\textstyle{1\over 4}})} < 0.4718617.$$

They also conjectured that the upper limit is actually the value of $B$,

$$\begin{eqnarray*} B&=&{1\over\sqrt{1+\sqrt{3}}} {\Gamma({\textstyle{1\over 3}})... ...2}})\over\Gamma({\textstyle{1\over 12}})}\\ &=&0.4718617\ldots \end{eqnarray*}$$

(Le Lionnais 1983).

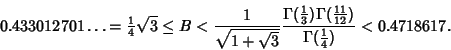
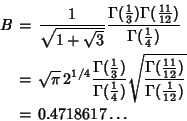
See also Landau Constant

References

Conway, J. B. Functions of One Complex Variable, 2nd ed. New York: Springer-Verlag, 1989.

Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/bloch/bloch.html

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 25, 1983.

Minda, C. D. ``Bloch Constants.'' J. d'Analyse Math. 41, 54-84, 1982.