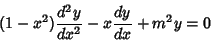 |
(1) |
for 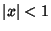 . The Chebyshev differential equation has regular Singularities at
. The Chebyshev differential equation has regular Singularities at
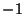 , 1, and
, 1, and 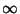 . It can be solved by series solution using the expansions
. It can be solved by series solution using the expansions
Now, plug (2-4) into the original equation (1) to obtain
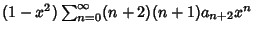
|
|
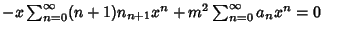
|
(5) |
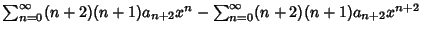
|
|
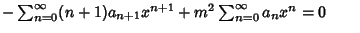
|
(6) |
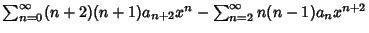
|
|
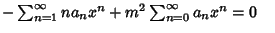
|
(7) |
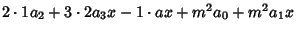
|
|
![$+\sum_{n=2}^\infty [(n+2)(n+1)a_{n+2} -n(n-1)a_n-na_n+m^2a_n]x^n=0\quad$](c1_1290.gif)
|
(8) |
![$(2a_2+m^2 a_0)+[(m^2-1)a_1+6a_3]x$](c1_1291.gif)
|
|
![$ +\sum_{n=2}^\infty [(n+2)(n+1)a_{n+2}+(m^2-n^2)a_n]x^n=0,\quad$](c1_1292.gif)
|
(9) |
so
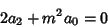 |
(10) |
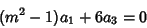 |
(11) |
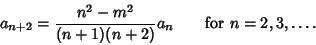 |
(12) |
The first two are special cases of the third, so the general recurrence relation
is
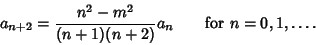 |
(13) |
From this, we obtain for the Even Coefficients
and for the Odd Coefficients
So the general solution is
![$y=a_0\left[{1+ \sum_{k=2, 4, \ldots}^\infty {[k^2-m^2][(k-2)^2-m^2]\cdots[-m^2]\over k!} x^k}\right]$](c1_1309.gif)
|
|
![$ +a_1\left[{x+\sum_{k=3, 5, \ldots}^\infty{[(k-2)^2-m^2][(k-2)^2-m^2]\cdots[1^2-m^2]\over k!} x^k}\right]\quad$](c1_1310.gif)
|
(20) |
If  is Even, then
is Even, then 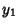 terminates and is a Polynomial solution, whereas if
terminates and is a Polynomial solution, whereas if 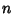 is Odd, then
is Odd, then 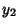 terminates and is
a Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the First
Kind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation
terminates and is
a Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the First
Kind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation
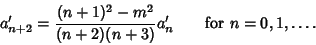 |
(21) |
© 1996-9 Eric W. Weisstein
1999-05-26
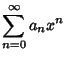
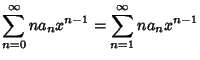
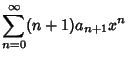
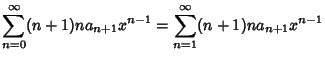
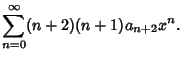
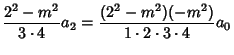
![$\displaystyle {[(2n)^2-m^2][(2n-2)^2-m^2]\cdots[-m^2]\over(2n)!} a_0,$](c1_1302.gif)
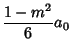
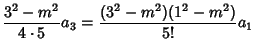
![$\displaystyle {[(2n-1)^2-m^2][(2n-3)^2-m^2]\cdots[1^2-m^2]\over(2n+1)!} a_1.$](c1_1308.gif)
![]() is Even, then
is Even, then ![]() terminates and is a Polynomial solution, whereas if
terminates and is a Polynomial solution, whereas if ![]() is Odd, then
is Odd, then ![]() terminates and is
a Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the First
Kind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation
terminates and is
a Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the First
Kind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation