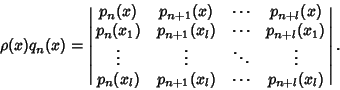Let 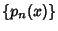 be orthogonal Polynomials associated with the distribution
be orthogonal Polynomials associated with the distribution 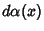 on the interval
on the interval ![$[a,b]$](c1_741.gif) . Also
let
. Also
let
(for 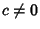 ) be a Polynomial of order
) be a Polynomial of order 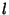 which is Nonnegative in this interval. Then the orthogonal Polynomials
which is Nonnegative in this interval. Then the orthogonal Polynomials
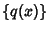 associated with the distribution
associated with the distribution
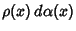 can be represented in terms of the Polynomials
can be represented in terms of the Polynomials 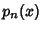 as
as
In the case of a zero 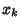 of multiplicity
of multiplicity 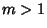 , we replace the corresponding rows by the derivatives of order 0, 1, 2,
...,
, we replace the corresponding rows by the derivatives of order 0, 1, 2,
..., 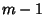 of the Polynomials
of the Polynomials 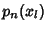 , ...,
, ..., 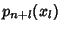 at
at 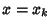 .
.
References
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 29-30, 1975.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be orthogonal Polynomials associated with the distribution
be orthogonal Polynomials associated with the distribution ![]() on the interval
on the interval ![]() . Also
let
. Also
let