Complete Sequence

A Sequence of numbers $V=\{\nu_n\}$ is complete if every Positive Integer $n$ is the sum of some subsequence of $V$, i.e., there exist $a_i=0$ or 1 such that

$$n=\sum_{i=1}^\infty a_i\nu_i$$

(Honsberger 1985, pp. 123-126). The Fibonacci Numbers are complete. In fact, dropping one number still leaves a complete sequence, although dropping two numbers does not (Honsberger 1985, pp. 123 and 126). The Sequence of Primes with the element $\{1\}$ prepended,

$$\{1, 2, 3, 5, 7, 11, 13, 17, 19, 23, \ldots\}$$

is complete, even if any number of Primes each $>7$ are dropped, as long as the dropped terms do not include two consecutive Primes (Honsberger 1985, pp. 127-128). This is a consequence of Bertrand's Postulate.

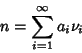
See also Bertrand's Postulate, Brown's Criterion, Fibonacci Dual Theorem, Greedy Algorithm, Weakly Complete Sequence, Zeckendorf's Theorem

References

Brown, J. L. Jr. ``Unique Representations of Integers as Sums of Distinct Lucas Numbers.'' Fib. Quart. 7, 243-252, 1969.

Hoggatt, V. E. Jr.; Cox, N.; and Bicknell, M. ``A Primer for Fibonacci Numbers. XII.'' Fib. Quart. 11, 317-331, 1973.

Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., 1985.