Cover

A group $C$ of Subsets of $X$ whose Union contains the given set $X$ ( $\cup \{S:S\in C\}=X$) is called a cover (or a Covering). A Minimal Cover is a cover for which removal of one member destroys the covering property. There are various types of specialized covers, including proper covers, antichain covers, minimal covers, $k$-covers, and $k^*$-covers. The number of possible covers for a set of $N$ elements is

$$\vert C(N)\vert = {1\over 2} \sum_{k=0}^N (-1)^k{N\choose k}2^{2^{N-k}},$$

the first few of which are 1, 5, 109, 32297, 2147321017, 9223372023970362989, ... (Sloane's A003465). The number of proper covers for a set of $N$ elements is

$$\vert C'(N)\vert = \vert C(N)\vert-{\textstyle{1\over 4}}2^{2^N}$$

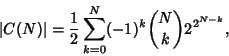
$$= \left[{{1\over 2} \sum_{k=0}^N (-1)^k{N\choose k}2^{2^{N-k}}}\right]-{2^{2^N}\over 4},$$

the first few of which are 0, 1, 45, 15913, 1073579193, ... (Sloane's A007537).

See also Minimal Cover

References

Eppstein, D. ``Covering and Packing.'' http://www.ics.uci.edu/~eppstein/junkyard/cover.html.

Macula, A. J. ``Covers of a Finite Set.'' Math. Mag. 67, 141-144, 1994.

Sloane, N. J. A. Sequences A003465/M4024 and A007537/M5287 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.