|
|
|
The ![]() Group is the Subgroup of the Gamma Group with
Group is the Subgroup of the Gamma Group with ![]() and
and
![]() Odd;
Odd; ![]() and
and ![]() Even. The function
Even. The function
| (1) |
| (2) |
![]() gives the value of the Modulus
gives the value of the Modulus
![]() for which the complementary and normal complete Elliptic Integrals of
the First Kind are related by
for which the complementary and normal complete Elliptic Integrals of
the First Kind are related by
| (3) |
| (4) |
| (5) |
From the definition of the lambda function,
| (6) |
| (7) | |||
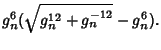 |
(8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
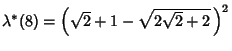
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
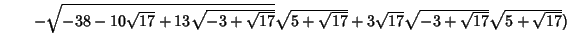
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
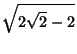 |
|||
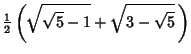 |
|||
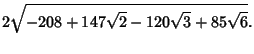 |
See also Elliptic Alpha Function, Elliptic Integral of the First Kind, Modulus (Elliptic Integral), Ramanujan g- and G-Functions, Theta Function
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 139 and 298, 1987.
Bowman, F. Introduction to Elliptic Functions, with Applications. New York: Dover, pp. 75, 95, and 98, 1961.
Selberg, A. and Chowla, S. ``On Epstein's Zeta-Function.'' J. Reine. Angew. Math. 227, 86-110, 1967.
Watson, G. N. ``Some Singular Moduli (1).'' Quart. J. Math. 3, 81-98, 1932.
|
|
|
© 1996-9 Eric W. Weisstein