Euler integration was defined by Schanuel and subsequently explored by Rota, Chen, and Klain. The Euler integral of a
Function
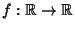 (assumed to be piecewise-constant with finitely many discontinuities) is the sum of
(assumed to be piecewise-constant with finitely many discontinuities) is the sum of
over the finitely many discontinuities of 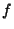 . The
. The 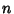 -D Euler integral can be defined for classes of functions
-D Euler integral can be defined for classes of functions
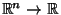 . Euler integration is additive, so the Euler integral of
. Euler integration is additive, so the Euler integral of 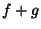 equals the sum of the Euler integrals of
equals the sum of the Euler integrals of
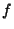 and
and 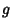 .
.
See also Euler Measure
© 1996-9 Eric W. Weisstein
1999-05-25
![]() (assumed to be piecewise-constant with finitely many discontinuities) is the sum of
(assumed to be piecewise-constant with finitely many discontinuities) is the sum of