Excircle

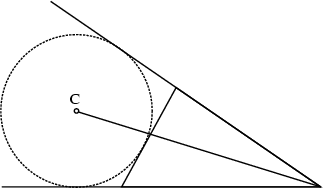
Given a Triangle, extend two nonadjacent sides. The Circle tangent to these two lines and to the other side of the Triangle is called an Escribed Circle, or excircle. The Center $J_i$ of the excircle is called the Excenter and lies on the external Angle Bisector of the opposite Angle. Every Triangle has three excircles, and the Trilinear Coordinates of the Excenters are $-1:1:1$, $1:-1:1$, and $1:1:-1$. The Radius $r_i$ of the excircle $i$ is called its Exradius.

Given a Triangle with Inradius $r$, let $h_i$ be the Altitudes of the excircles, and $r_i$ their Radii (the Exradii). Then

$${1\over h_1}+{1\over h_2}+{1\over h_3}={1\over r_1}+{1\over r_2}+{1\over r_3}={1\over r}$$

(Johnson 1929, p. 189).

See also Excenter, Excenter-Excenter Circle, Excentral Triangle, Feuerbach's Theorem, Nagel Point, Triangle Transformation Principle

References

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 11-13, 1967.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 176-177 and 182-194, 1929.