Let 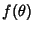 be Lebesgue Integrable and let
be Lebesgue Integrable and let
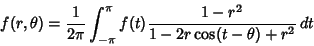 |
(1) |
be the corresponding Poisson Integral. Then Almost Everywhere in
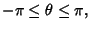
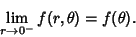 |
(2) |
Let
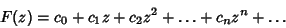 |
(3) |
be regular for 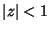 , and let the integral
, and let the integral
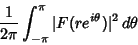 |
(4) |
be bounded for 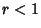 . This condition is equivalent to the convergence of
. This condition is equivalent to the convergence of
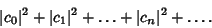 |
(5) |
Then almost everywhere in
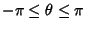 ,
,
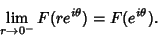 |
(6) |
Furthermore,
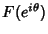 is measurable,
is measurable,
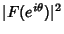 is Lebesgue Integrable, and the Fourier
Series of
is Lebesgue Integrable, and the Fourier
Series of
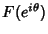 is given by writing
is given by writing 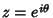 .
.
References
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., p. 274, 1975.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be Lebesgue Integrable and let
be Lebesgue Integrable and let