|
|
|
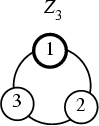
The unique group of Order 3. It is both Abelian and Cyclic. Examples include the Point Groups ![]() and
and ![]() and the integers under addition modulo 3. The elements
and the integers under addition modulo 3. The elements ![]() of the group satisfy
of the group satisfy ![]() where 1 is the Identity Element. The Cycle Graph is shown above, and the
Multiplication Table is given below.
where 1 is the Identity Element. The Cycle Graph is shown above, and the
Multiplication Table is given below.
| 1 | |||
| 1 | 1 | ||
| 1 | |||
| 1 |
The Conjugacy Classes are ![]() ,
, ![]() ,
,
| 1 | |||
| 1 | 1 | 1 | |
| 1 | 1 | ||
| 1 | 1 |