|
|
|
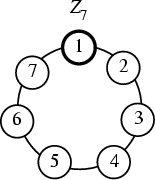
The unique Group of Order 7. It is Abelian and
Cyclic. Examples include the Point Group ![]() and the integers modulo 7
under addition. The elements
and the integers modulo 7
under addition. The elements ![]() of the group satisfy
of the group satisfy ![]() , where 1 is the Identity Element.
The Cycle Graph is shown above.
, where 1 is the Identity Element.
The Cycle Graph is shown above.
| 1 | |||||||
| 1 | 1 | ||||||
| 1 | |||||||
| 1 | |||||||
| 1 | |||||||
| 1 | |||||||
| 1 | |||||||
| 1 |
The Conjugacy Classes are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.