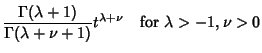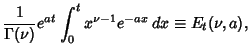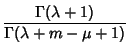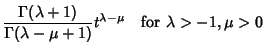Denote the  th Derivative
th Derivative 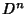 and the
and the  -fold Integral
-fold Integral 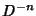 . Then
. Then
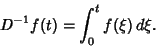 |
(1) |
Now, if
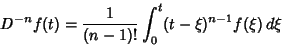 |
(2) |
is true for  , then
, then
Interchanging the order of integration gives
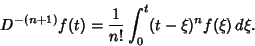 |
(4) |
But (2) is true for  , so it is also true for all
, so it is also true for all  by Induction. The fractional integral of
by Induction. The fractional integral of
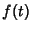 can then be defined by
can then be defined by
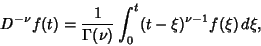 |
(5) |
where 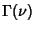 is the Gamma Function.
is the Gamma Function.
The fractional integral can only be given in terms of elementary functions for a small number of functions. For
example,
where 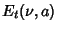 is the Et-Function. The fractional derivative of
is the Et-Function. The fractional derivative of 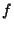 (if it exists) can be defined by
(if it exists) can be defined by
![\begin{displaymath}
D^\mu f(t)=D^m[D^{-(m-\mu)}f(t)].
\end{displaymath}](f_1945.gif) |
(8) |
An example is
It is always true that, for 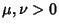 ,
,
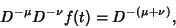 |
(11) |
but not always true that
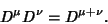 |
(12) |
See also Derivative, Integral
References
Love, E. R. ``Fractional Derivatives of Imaginary Order.'' J. London Math. Soc. 3, 241-259, 1971.
McBride, A. C. Fractional Calculus. New York: Halsted Press, 1986.
Miller, K. S. ``Derivatives of Noninteger Order.'' Math. Mag. 68, 183-192, 1995.
Nishimoto, K. Fractional Calculus. New Haven, CT: University of New Haven Press, 1989.
Spanier, J. and Oldham, K. B. The Fractional Calculus. New York: Academic Press, 1974.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() th Derivative
th Derivative ![]() and the
and the ![]() -fold Integral
-fold Integral ![]() . Then
. Then
![$\displaystyle D^{-1}\left[{{1\over(n-1)!} \int_0^t (t-\xi)^{n-1}f(\xi)\,d\xi}\right]$](f_1934.gif)
![$\displaystyle \int_0^t \left[{{1\over(n-1)!}\int_0^x (x-\xi)^{n-1}f(\xi)\,d\xi}\right]\,dx.$](f_1935.gif)