In physics, the Fresnel integrals are most often defined by
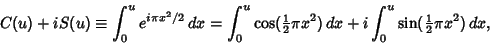 |
(1) |
so
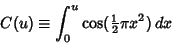 |
(2) |
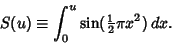 |
(3) |
They satisfy
Related functions are defined as
An asymptotic expansion for 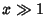 gives
gives
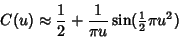 |
(10) |
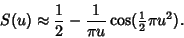 |
(11) |
Therefore, as 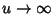 ,
, 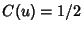 and
and 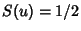 . The Fresnel integrals are sometimes alternatively
defined as
. The Fresnel integrals are sometimes alternatively
defined as
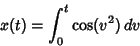 |
(12) |
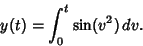 |
(13) |
Letting 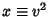 so
so
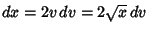 , and
, and
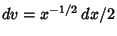
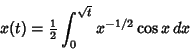 |
(14) |
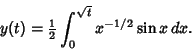 |
(15) |
In this form, they have a particularly simple expansion in terms of Spherical Bessel Functions of the First
Kind. Using
where 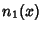 is a Spherical Bessel Function of the Second Kind
is a Spherical Bessel Function of the Second Kind
See also Cornu Spiral
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Fresnel Integrals.''
§7.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 300-302, 1972.
Leonard, I. E. ``More on Fresnel Integrals.'' Amer. Math. Monthly 95, 431-433, 1988.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Fresnel Integrals, Cosine and Sine Integrals.'' §6.79 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 248-252, 1992.
Spanier, J. and Oldham, K. B. ``The Fresnel Integrals 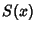 and
and 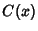 .''
Ch. 39 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 373-383, 1987.
.''
Ch. 39 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 373-383, 1987.
© 1996-9 Eric W. Weisstein
1999-05-26
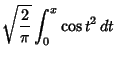
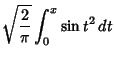
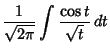
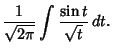
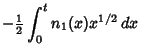
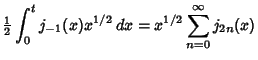

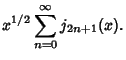
![]() and
and ![]() .''
Ch. 39 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 373-383, 1987.
.''
Ch. 39 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 373-383, 1987.