A generalization of the Fibonacci Numbers defined by
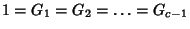 and the Recurrence Relation
and the Recurrence Relation
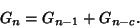 |
(1) |
These are the sums of elements on successive diagonals of a left-justified Pascal's Triangle beginning in the left-most
column and moving in steps of 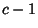 up and 1 right. The case
up and 1 right. The case 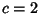 equals the usual Fibonacci Number. These numbers
satisfy the identities
equals the usual Fibonacci Number. These numbers
satisfy the identities
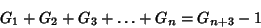 |
(2) |
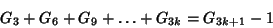 |
(3) |
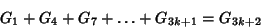 |
(4) |
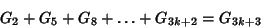 |
(5) |
(Bicknell-Johnson and Spears 1996). For the special case 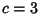 ,
,
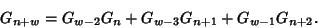 |
(6) |
Bicknell-Johnson and Spears (1996) give many further identities.
Horadam (1965) defined the generalized Fibonacci numbers 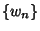 as
as
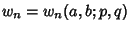 , where
, where  ,
,  ,
,  , and
, and  are Integers,
are Integers, 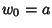 ,
, 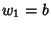 , and
, and
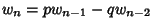 for
for  . They satisfy the identities
. They satisfy the identities
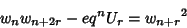 |
(7) |
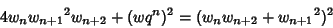 |
(8) |
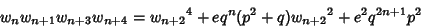 |
(9) |
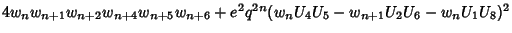
|
|
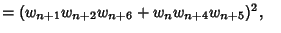
|
(10) |
where
The final above result is due to Morgado (1987) and is called the Morgado Identity.
Another generalization of the Fibonacci numbers is denoted  . Given
. Given  and
and  , define the generalized Fibonacci
number by
, define the generalized Fibonacci
number by
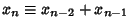 for
for  ,
,
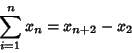 |
(13) |
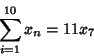 |
(14) |
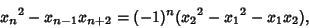 |
(15) |
where the plus and minus signs alternate.
See also Fibonacci Number
References
Bicknell, M. ``A Primer for the Fibonacci Numbers, Part VIII: Sequences of Sums from Pascal's Triangle.''
Fib. Quart. 9, 74-81, 1971.
Bicknell-Johnson, M. and Spears, C. P. ``Classes of Identities for the Generalized Fibonacci Numbers
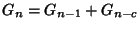 for Matrices with Constant Valued Determinants.'' Fib. Quart. 34, 121-128, 1996.
for Matrices with Constant Valued Determinants.'' Fib. Quart. 34, 121-128, 1996.
Dujella, A. ``Generalized Fibonacci Numbers and the Problem of Diophantus.'' Fib. Quart. 34, 164-175, 1996.
Horadam, A. F. ``Generating Functions for Powers of a Certain Generalized Sequence of Numbers.'' Duke Math. J. 32, 437-446, 1965.
Horadam, A. F. ``Generalization of a Result of Morgado.'' Portugaliae Math. 44, 131-136, 1987.
Horadam, A. F. and Shannon, A. G. ``Generalization of Identities of Catalan and Others.'' Portugaliae Math. 44, 137-148, 1987.
Morgado, J. ``Note on Some Results of A. F. Horadam and A. G. Shannon Concerning a Catalan's Identity on Fibonacci Numbers.''
Portugaliae Math. 44, 243-252, 1987.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and the Recurrence Relation
and the Recurrence Relation
![]() as
as
![]() , where
, where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are Integers,
are Integers, ![]() ,
, ![]() , and
, and
![]() for
for ![]() . They satisfy the identities
. They satisfy the identities
![]() . Given
. Given ![]() and
and ![]() , define the generalized Fibonacci
number by
, define the generalized Fibonacci
number by
![]() for
for ![]() ,
,
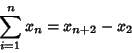
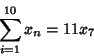
![]() for Matrices with Constant Valued Determinants.'' Fib. Quart. 34, 121-128, 1996.
for Matrices with Constant Valued Determinants.'' Fib. Quart. 34, 121-128, 1996.