|
|
|
A helix is also called a Curve of Constant Slope. It can be defined as a curve for which the Tangent makes
a constant Angle with a fixed line. The helix is a Space Curve with parametric equations
| (1) | |||
| (2) | |||
| (3) |
| (4) |
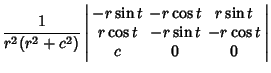
| (5) |
 |
|||
| (6) |
| (7) |
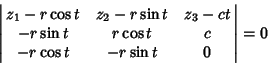 |
(8) |
| (9) |
The Minimal Surface of a helix is a Helicoid.
See also Generalized Helix, Helicoid, Spherical Helix
References
Geometry Center. ``The Helix.''
http://www.geom.umn.edu/zoo/diffgeom/surfspace/helicoid/helix.html.
Gray, A. ``The Helix and Its Generalizations.'' §7.5 in
Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 138-140, 1993.
Isenberg, C. Plate 4.11 in The Science of Soap Films and Soap Bubbles. New York: Dover, 1992.
Pappas, T. ``The Helix--Mathematics & Genetics.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra,
pp. 166-168, 1989.
Wolfram, S. The Mathematica Book, 3rd ed. Champaign, IL: Wolfram Media, p. 163, 1996.
|
|
|
© 1996-9 Eric W. Weisstein