A Hermitian Operator 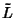 is one which satisfies
is one which satisfies
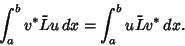 |
(1) |
As shown in Sturm-Liouville Theory, if 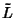 is Self-Adjoint and satisfies
the boundary conditions
is Self-Adjoint and satisfies
the boundary conditions
![\begin{displaymath}[v^*pu']_{x=a} = [v^*pu']_{x=b},
\end{displaymath}](h_1483.gif) |
(2) |
then it is automatically Hermitian. Hermitian operators have Real Eigenvalues,
Orthogonal Eigenfunctions, and the corresponding
Eigenfunctions form a Complete set when 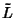 is second-order and
linear. In order to prove that Eigenvalues must be Real and
Eigenfunctions Orthogonal, consider
is second-order and
linear. In order to prove that Eigenvalues must be Real and
Eigenfunctions Orthogonal, consider
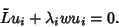 |
(3) |
Assume there is a second Eigenvalue 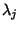 such that
such that
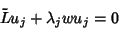 |
(4) |
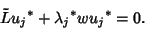 |
(5) |
Now multiply (3) by 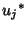 and (5) by
and (5) by 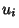
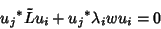 |
(6) |
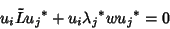 |
(7) |
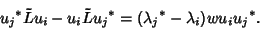 |
(8) |
Now integrate
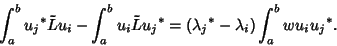 |
(9) |
But because 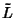 is Hermitian, the left side vanishes.
is Hermitian, the left side vanishes.
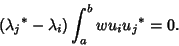 |
(10) |
If Eigenvalues 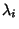 and
and 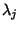 are not degenerate, then
are not degenerate, then
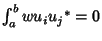 , so the
Eigenfunctions are Orthogonal. If the
Eigenvalues are degenerate, the Eigenfunctions are not necessarily
orthogonal. Now take
, so the
Eigenfunctions are Orthogonal. If the
Eigenvalues are degenerate, the Eigenfunctions are not necessarily
orthogonal. Now take  .
.
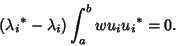 |
(11) |
The integral cannot vanish unless 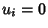 , so we have
, so we have
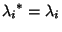 and the Eigenvalues
are real.
and the Eigenvalues
are real.
For a Hermitian operator 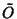 ,
,
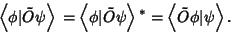 |
(12) |
In integral notation,
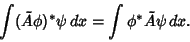 |
(13) |
Given Hermitian operators 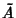 and
and 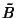 ,
,
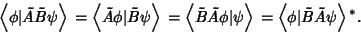 |
(14) |
Because, for a Hermitian operator 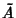 with Eigenvalue
with Eigenvalue  ,
,
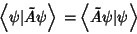 |
(15) |
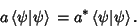 |
(16) |
Therefore, either
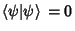 or
or 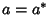 . But
. But
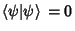 Iff
Iff 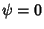 , so
, so
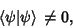 |
(17) |
for a nontrivial Eigenfunction. This means that 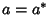 , namely that Hermitian operators produce Real expectation values. Every observable must therefore have a corresponding Hermitian operator. Furthermore,
, namely that Hermitian operators produce Real expectation values. Every observable must therefore have a corresponding Hermitian operator. Furthermore,
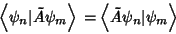 |
(18) |
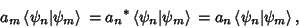 |
(19) |
since 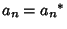 . Then
. Then
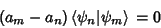 |
(20) |
For 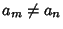 (i.e.,
(i.e.,
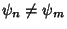 ),
),
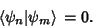 |
(21) |
For 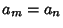 (i.e.,
(i.e.,
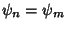 ),
),
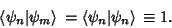 |
(22) |
Therefore,
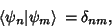 |
(23) |
so the basis of Eigenfunctions corresponding to a Hermitian operator are Orthonormal. Given two Hermitian operators 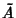 and
and 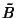 ,
,
![\begin{displaymath}
(\tilde A \tilde B )^\dagger =\tilde B^\dagger\tilde A^\dagger
= \tilde B\tilde A =\tilde A \tilde B +[\tilde B ,\tilde A ],
\end{displaymath}](h_1524.gif) |
(24) |
the operator
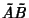 equals
equals
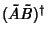 , and is therefore
Hermitian, only if
, and is therefore
Hermitian, only if
![\begin{displaymath}[\tilde B, \tilde A]= 0.
\end{displaymath}](h_1527.gif) |
(25) |
Given an arbitrary operator 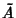 ,
,
so
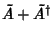 is Hermitian.
is Hermitian.
so
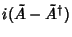 is Hermitian. Similarly,
is Hermitian. Similarly,
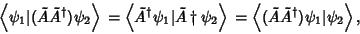 |
(28) |
so
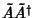 is Hermitian.
is Hermitian.
Define the Hermitian conjugate operator
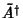 by
by
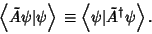 |
(29) |
For a Hermitian operator,
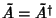 . Furthermore, given two Hermitian operators
. Furthermore, given two Hermitian operators 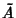 and
and 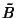 ,
,
so
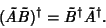 |
(31) |
By further iterations, this can be generalized to
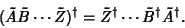 |
(32) |
See also Adjoint Operator, Hermitian Matrix, Self-Adjoint Operator,
Sturm-Liouville Theory
References
Arfken, G. ``Hermitian (Self-Adjoint) Operators.'' §9.2 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 504-506 and 510-516, 1985.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() is one which satisfies
is one which satisfies
![]() ,
,
![]() by
by