Hexagonal Number

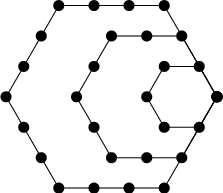
A Figurate Number and 6-Polygonal Number of the form $n(2n-1)$. The first few are 1, 6, 15, 28, 45, ... (Sloane's A000384). The Generating Function of the hexagonal numbers

$${x(3x+1)\over(1-x)^3}=x+6x^2+15x^3+28x^4+\ldots.$$

Every hexagonal number is a Triangular Number since

$$r(2r-1)={\textstyle{1\over 2}}(2r-1)[(2r-1)+1].$$

In 1830, Legendre (1979) proved that every number larger than 1791 is a sum of four hexagonal numbers, and Duke and Schulze-Pillot (1990) improved this to three hexagonal numbers for every sufficiently large integer. The numbers 11 and 26 can only be represented as a sum using the maximum possible of six hexagonal numbers:

$$11 = 1+1+1+1+1+6$$

$$26 = 1+1+6+6+6+6.$$

See also Figurate Number, Hex Number, Triangular Number

References

Duke, W. and Schulze-Pillot, R. ``Representations of Integers by Positive Ternary Quadratic Forms and Equidistribution of Lattice Points on Ellipsoids.'' Invent. Math. 99, 49-57, 1990.

Guy, R. K. ``Sums of Squares.'' §C20 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138, 1994.

Legendre, A.-M. Théorie des nombres, 4th ed., 2 vols. Paris: A. Blanchard, 1979.

Sloane, N. J. A. Sequence A000384/M4108 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.