|
|
|
A point where a stable and an unstable separatrix (invariant manifold) from the same fixed point or same family intersect.
Therefore, the limits
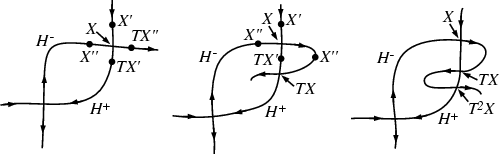
Refer to the above figure. Let ![]() be the point of intersection, with
be the point of intersection, with ![]() ahead of
ahead of ![]() on one Manifold and
on one Manifold and ![]() ahead of
ahead of ![]() of the other. The mapping of each of these points
of the other. The mapping of each of these points ![]() and
and ![]() must be ahead of the mapping of
must be ahead of the mapping of ![]() ,
, ![]() .
The only way this can happen is if the Manifold loops back and crosses itself at a new homoclinic point. Another
loop must be formed, with
.
The only way this can happen is if the Manifold loops back and crosses itself at a new homoclinic point. Another
loop must be formed, with ![]() another homoclinic point. Since
another homoclinic point. Since ![]() is closer to the hyperbolic point than
is closer to the hyperbolic point than ![]() , the
distance between
, the
distance between ![]() and
and ![]() is less than that between
is less than that between ![]() and
and ![]() . Area preservation requires the Area to
remain the same, so each new curve (which is closer than the previous one) must extend further. In effect, the loops
become longer and thinner. The network of curves leading to a dense Area of homoclinic points is known as a
homoclinic tangle or tendril. Homoclinic points appear where Chaotic regions touch in a hyperbolic
Fixed Point.
. Area preservation requires the Area to
remain the same, so each new curve (which is closer than the previous one) must extend further. In effect, the loops
become longer and thinner. The network of curves leading to a dense Area of homoclinic points is known as a
homoclinic tangle or tendril. Homoclinic points appear where Chaotic regions touch in a hyperbolic
Fixed Point.
A small Disk centered near a homoclinic point includes infinitely many periodic points of different periods.
Poincaré ![]() showed that if there is a single homoclinic point, there are an infinite number. More
specifically, there are infinitely many homoclinic points in each small disk (Nusse and Yorke 1996).
showed that if there is a single homoclinic point, there are an infinite number. More
specifically, there are infinitely many homoclinic points in each small disk (Nusse and Yorke 1996).
See also Heteroclinic Point, Manifold, Separatrix
References
Nusse, H. E. and Yorke, J. A. ``Basins of Attraction.'' Science 271, 1376-1380, 1996.
Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, p. 145,
1989.
|
|
|
© 1996-9 Eric W. Weisstein