|
|
|
The hyperbolic functions sinh, cosh, tanh, csch, sech, coth (Hyperbolic Sine, Hyperbolic Cosine, etc.) share many
properties with the corresponding Circular Functions. The hyperbolic functions arise in many problems of mathematics
and mathematical physics in which integrals involving ![]() arise (whereas the Circular Functions involve
arise (whereas the Circular Functions involve
![]() ).
).
For instance, the Hyperbolic Sine arises in the
gravitational potential of a cylinder ![]() and the calculation of the
Roche limit.
and the calculation of the
Roche limit. ![]() The
Hyperbolic Cosine function is the shape of a hanging cable (the so-called Catenary). The Hyperbolic
Tangent arises in the calculation of magnetic moment
The
Hyperbolic Cosine function is the shape of a hanging cable (the so-called Catenary). The Hyperbolic
Tangent arises in the calculation of magnetic moment ![]() and rapidity
and rapidity ![]() of
special relativity.
of
special relativity. ![]() All three appear in the
Schwarzschild metric using external isotropic Kruskal coordinates
All three appear in the
Schwarzschild metric using external isotropic Kruskal coordinates ![]() in
general relativity.
in
general relativity. ![]() The Hyperbolic Secant arises in the profile of a laminar
jet.
The Hyperbolic Secant arises in the profile of a laminar
jet. ![]() The Hyperbolic Cotangent arises in the Langevin function
The Hyperbolic Cotangent arises in the Langevin function ![]() for magnetic polarization.
for magnetic polarization. ![]()
The hyperbolic functions are defined by
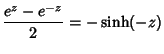 |
(1) | ||
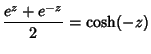 |
(2) | ||
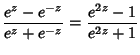 |
(3) | ||
| (4) | |||
| (5) | |||
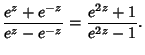 |
(6) |
| (7) |
| (8) |
| (9) | |||
| (10) | |||
| (11) |
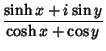 |
(12) | ||
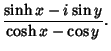 |
(13) |
| (14) | |||
| (15) |
Identities for Complex arguments include
| (16) | |||
| (17) |
| (18) | |||
| (19) |
Integrals involving hyperbolic functions include
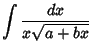 |
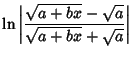 |
(20) | |
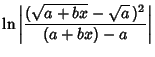 |
|||
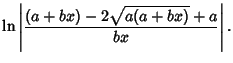 |
|||
| (21) |
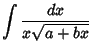 |
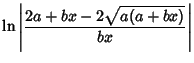 |
(22) | |
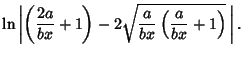 |
|||
| (23) |
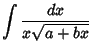 |
![$\displaystyle \ln\left[{z-2\sqrt{{\textstyle{1\over 2}}(z-1){\textstyle{1\over 2}}(z+1)}\,}\right]$](h_2071.gif) |
||
| (24) | |||
| (25) | |||
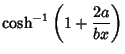 |
(26) | ||
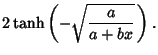 |
(27) |
See also Hyperbolic Cosecant, Hyperbolic Cosine, Hyperbolic Cotangent, Generalized Hyperbolic Functions, Hyperbolic Inverse Functions, Hyperbolic Secant, Hyperbolic Sine, Hyperbolic Tangent, Hyperbolic Inverse Functions, Osborne's Rule
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Hyperbolic Functions.'' §4.5 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 83-86, 1972.
Beyer, W. H. ``Hyperbolic Function.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press,
pp. 168-186, 1987.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 126-131, 1967.
Yates, R. C. ``Hyperbolic Functions.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 113-118, 1952.
|
|
|
© 1996-9 Eric W. Weisstein