An infinitesimal transformation of a Vector 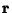 is given by
is given by
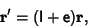 |
(1) |
where the Matrix
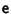 is infinitesimal and I is the Identity Matrix. (Note that the infinitesimal
transformation may not correspond to an inversion, since inversion is a discontinuous process.) The
Commutativity of infinitesimal transformations
is infinitesimal and I is the Identity Matrix. (Note that the infinitesimal
transformation may not correspond to an inversion, since inversion is a discontinuous process.) The
Commutativity of infinitesimal transformations
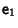 and
and
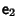 is established by the
equivalence of
is established by the
equivalence of
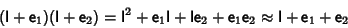 |
(2) |
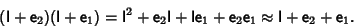 |
(3) |
Now let
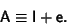 |
(4) |
The inverse
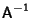 is then
is then
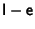 , since
, since
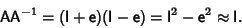 |
(5) |
Since we are defining our infinitesimal transformation to be a rotation, Orthogonality
of Rotation Matrices
requires that
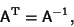 |
(6) |
but
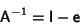 |
(7) |
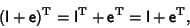 |
(8) |
so
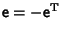 and the infinitesimal rotation is Antisymmetric. It must therefore have
a Matrix of the form
and the infinitesimal rotation is Antisymmetric. It must therefore have
a Matrix of the form
![\begin{displaymath}
{\hbox{\sf e}} = \left[{\matrix{
0 & d\Omega_3 & -d\Omega_2...
..._3 & 0 & d\Omega_1\cr
d\Omega_2 & -d\Omega_1 & 0\cr}}\right].
\end{displaymath}](i_502.gif) |
(9) |
The differential change in a vector  upon application of the Rotation Matrix is then
upon application of the Rotation Matrix is then
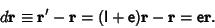 |
(10) |
Writing in Matrix form,
Therefore,
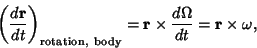 |
(13) |
where
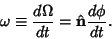 |
(14) |
The total rotation observed in the stationary frame will be a sum of the rotational velocity and the velocity in the
rotating frame. However, note that an observer in the stationary frame will see a velocity opposite in direction to that
of the observer in the frame of the rotating body, so
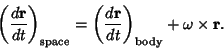 |
(15) |
This can be written as an operator equation, known as the Rotation Operator, defined as
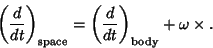 |
(16) |
See also Acceleration, Euler Angles, Rotation, Rotation Matrix, Rotation Operator
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is given by
is given by
![\begin{displaymath}
{\hbox{\sf e}} = \left[{\matrix{
0 & d\Omega_3 & -d\Omega_2...
..._3 & 0 & d\Omega_1\cr
d\Omega_2 & -d\Omega_1 & 0\cr}}\right].
\end{displaymath}](i_502.gif)
![$\displaystyle \left[\begin{array}{c}x\\ y\\ z\end{array}\right]\left[\begin{a...
...2\\ -d\Omega_3 & 0 & d\Omega_1\\ d\Omega_2 & -d\Omega_1 & 0\end{array}\right]$](i_505.gif)
![$\displaystyle \left[\begin{array}{c} y\,d\Omega_3-z\,d\Omega_2\\ z\,d\Omega_1-x\,d\Omega_3\\ x\,d\Omega_2-y\,d\Omega_1\end{array}\right]$](i_506.gif)