|
|
|
Jackson's theorem is a statement about the error ![]() of the best uniform approximation to a Real Function
of the best uniform approximation to a Real Function ![]() on
on ![]() by Real Polynomials of degree at most
by Real Polynomials of degree at most ![]() . Let
. Let ![]() be of bounded variation in
be of bounded variation in ![]() and let
and let ![]() and
and ![]() denote the least upper bound of
denote the least upper bound of ![]() and the total variation of
and the total variation of
![]() in
in ![]() , respectively. Given the function
, respectively. Given the function
| (1) |
| (2) |
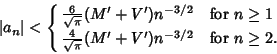 |
(3) |
Bernstein strengthened Jackson's theorem to
| (4) |
| (5) |
| (6) |
See also Legendre Series, Picone's Theorem
References
Cheney, E. W. Introduction to Approximation Theory. New York: McGraw-Hill, 1966.
Jackson, D. The Theory of Approximation. New York: Amer. Math. Soc., p. 76, 1930.
Rivlin, T. J. An Introduction to the Approximation of Functions. New York: Dover, 1981.
Sansone, G. Orthogonal Functions, rev. English ed. New York: Dover, pp. 205-208, 1991.