Jinc Function

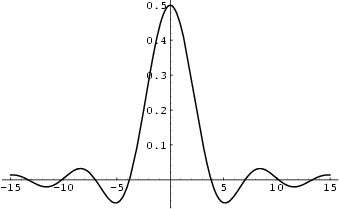
The jinc function is defined as

$$\mathop{\rm jinc}\nolimits (x)\equiv {J_1(x)\over x},$$

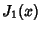where $J_1(x)$ is a Bessel Function of the First Kind, and satisfies $\lim_{x\to 0}\mathop{\rm jinc}\nolimits (x)=1/2$. The Derivative of the jinc function is given by

$$\mathop{\rm jinc}\nolimits '(x)=-{J_2(x)\over x}.$$

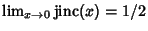The function is sometimes normalized by multiplying by a factor of 2 so that 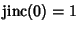$\mathop{\rm jinc}\nolimits (0)=1$ (Siegman 1986, p. 729).

See also Bessel Function of the First Kind, Sinc Function

References

Siegman, A. E. Lasers. Sausalito, CA: University Science Books, 1986.