Kummer's first formula is
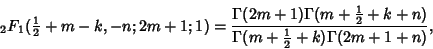 |
(1) |
where
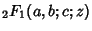 is the Hypergeometric Function with
is the Hypergeometric Function with 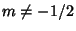 ,
, 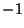 ,
, 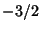 , ..., and
, ..., and 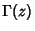 is the
Gamma Function. The identity can be written in the more symmetrical form as
is the
Gamma Function. The identity can be written in the more symmetrical form as
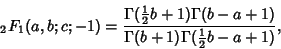 |
(2) |
where 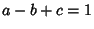 and
and 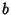 is a positive integer. If
is a positive integer. If 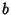 is a negative integer, the identity takes the form
is a negative integer, the identity takes the form
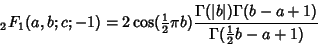 |
(3) |
(Petkovsek et al. 1996).
Kummer's second formula is
![\begin{displaymath}
{}_1F_1({\textstyle{1\over 2}}+m;2m+1;z) = M_{0,m}(z) = z^{m...
...^\infty {z^{2p}\over 2^{4p} p!(m+1)(m+2)\cdots (m+p)}}\right],
\end{displaymath}](k_896.gif) |
(4) |
where
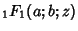 is the Confluent Hypergeometric Function and
is the Confluent Hypergeometric Function and 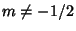 ,
, 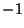 ,
, 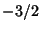 , ....
, ....
References
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, pp. 42-43 and 126, 1996.
© 1996-9 Eric W. Weisstein
1999-05-26
![\begin{displaymath}
{}_1F_1({\textstyle{1\over 2}}+m;2m+1;z) = M_{0,m}(z) = z^{m...
...^\infty {z^{2p}\over 2^{4p} p!(m+1)(m+2)\cdots (m+p)}}\right],
\end{displaymath}](k_896.gif)