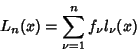Let 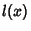 be an
be an  th degree Polynomial with zeros at
th degree Polynomial with zeros at 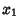 , ...,
, ..., 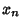 . Then the fundamental
Polynomials are
. Then the fundamental
Polynomials are
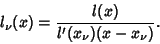 |
(1) |
They have the property
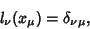 |
(2) |
where
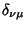 is the Kronecker Delta.
Now let
is the Kronecker Delta.
Now let 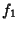 , ...,
, ..., 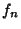 be values. Then the expansion
be values. Then the expansion
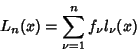 |
(3) |
gives the unique Lagrange Interpolating Polynomial assuming the values 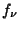 at
at 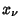 . Let
. Let
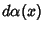 be an arbitrary distribution on the interval
be an arbitrary distribution on the interval ![$[a,b]$](l1_96.gif) ,
, 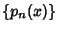 the associated Orthogonal
Polynomials, and
the associated Orthogonal
Polynomials, and 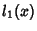 , ...,
, ..., 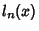 the fundamental Polynomials corresponding to the
set of zeros of
the fundamental Polynomials corresponding to the
set of zeros of 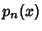 . Then
. Then
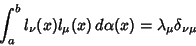 |
(4) |
for 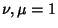 , 2, ...,
, 2, ...,  , where
, where 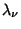 are Christoffel Numbers.
are Christoffel Numbers.
References
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI:
Amer. Math. Soc., pp. 329 and 332, 1975.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be an
be an ![]() th degree Polynomial with zeros at
th degree Polynomial with zeros at ![]() , ...,
, ..., ![]() . Then the fundamental
Polynomials are
. Then the fundamental
Polynomials are