Limaçon

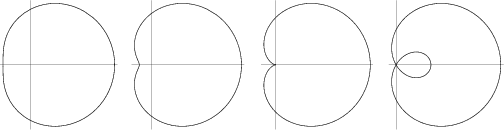
The limaçon is a polar curve of the form

$$r=b+a\cos\theta$$

also called the Limaçon of Pascal. It was first investigated by Dürer, who gave a method for drawing it in Underweysung der Messung (1525). It was rediscovered by Étienne Pascal, father of Blaise Pascal, and named by Gilles-Personne Roberval in 1650 (MacTutor Archive). The word ``limaçon'' comes from the Latin limax, meaning ``snail.''

If $b\geq 2a$, we have a convex limaçon. If $2a>b>a$, we have a dimpled limaçon. If $b=a$, the limaçon degenerates to a Cardioid. If $b<a$, we have limaçon with an inner loop. If $b=a/2$, it is a Trisectrix (but not the Maclaurin Trisectrix) with inner loop of Area

$$A_{\rm inner\ loop}={\textstyle{1\over 4}}a^2\left({\pi-3\sqrt{3\over 2}\,}\right),$$

and Area between the loops of

$$A_{\rm between\ loops}={\textstyle{1\over 4}}a^2(\pi+3\sqrt{3}\,)$$

(MacTutor Archive). The limaçon is an Anallagmatic Curve, and is also the Catacaustic of a Circle when the Radiant Point is a finite (Nonzero) distance from the Circumference, as shown by Thomas de St. Laurent in 1826 (MacTutor Archive).

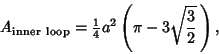
See also Cardioid

References

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 113-117, 1972.

Lee, X. ``Limacon of Pascal.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/LimaconOfPascal_dir/limaconOfPascal.html

Lee, X. ``Limacon Graphics Gallery.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/LimaconGGallery_dir/limaconGGallery.html

Lockwood, E. H. ``The Limaçon.'' Ch. 5 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 44-51, 1967.

MacTutor History of Mathematics Archive. ``Limacon of Pascal.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Limacon.html.

Yates, R. C. ``Limacon of Pascal.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 148-151, 1952.