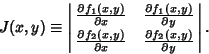Given a Lyapunov Characteristic Exponent 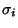 , the corresponding Lyapunov characteristic number
, the corresponding Lyapunov characteristic number 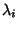 is defined as
is defined as
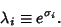 |
(1) |
For an  -dimensional linear Map,
-dimensional linear Map,
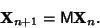 |
(2) |
The Lyapunov characteristic numbers 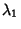 , ...,
, ..., 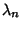 are the Eigenvalues of the Map
Matrix. For an arbitrary Map
are the Eigenvalues of the Map
Matrix. For an arbitrary Map
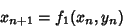 |
(3) |
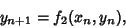 |
(4) |
the Lyapunov numbers are the Eigenvalues of the limit
![\begin{displaymath}
\lim_{n\to\infty} [J(x_n,y_n)J(x_{n-1},y_{n-1})\cdots J(x_1,y_1)]^{1/n},
\end{displaymath}](l2_1264.gif) |
(5) |
where 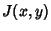 is the Jacobian
is the Jacobian
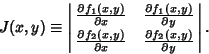 |
(6) |
If 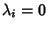 for all
for all 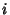 , the system is not Chaotic. If
, the system is not Chaotic. If
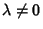 and the Map is
Area-Preserving (Hamiltonian), the product of
Eigenvalues is 1.
and the Map is
Area-Preserving (Hamiltonian), the product of
Eigenvalues is 1.
See also Adiabatic Invariant, Chaos, Lyapunov Characteristic Exponent
© 1996-9 Eric W. Weisstein
1999-05-25
![]() , the corresponding Lyapunov characteristic number
, the corresponding Lyapunov characteristic number ![]() is defined as
is defined as