Orthic Triangle

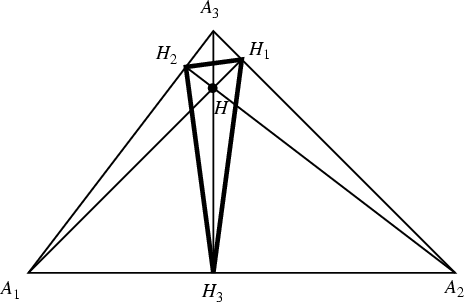
Given a Triangle $\Delta A_1A_2A_3$, the Triangle $\Delta H_1H_2H_3$ with Vertices at the feet of the Altitudes (perpendiculars from a point to the sides) is called the orthic triangle. The three lines $A_iH_i$ are Concurrent at the Orthocenter $H$ of $\Delta A_1A_2A_3$.

The centroid of the orthic triangle has Triangle Center Function

$$\alpha=a^2\cos(B-C)$$

(Casey 1893, Kimberling 1994). The Orthocenter of the orthic triangle has Triangle Center Function

$$\alpha=\cos(2A)\cos(B-C)$$

(Casey 1893, Kimberling 1994). The Symmedian Point of the orthic triangle has Triangle Center Function

$$\alpha=\tan A\cos(B-C)$$

(Casey 1893, Kimberling 1994).

See also Altitude, Fagnano's Problem, Orthocenter, Pedal Triangle, Schwarz's Triangle Problem, Symmedian Point

References

Casey, J. A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., p. 9, 1893.

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 9 and 16-18, 1967.

Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.