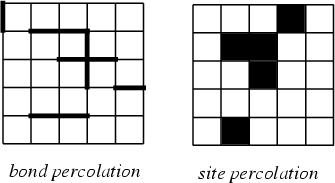
|
|
|
Percolation theory deals with fluid flow (or any other similar process) in random media. If the medium is a set of regular Lattice Points, then there are two types of percolation. A Site Percolation considers the lattice vertices as the relevant entities; a Bond Percolation considers the lattice edges as the relevant entities.
See also Bond Percolation, Cayley Tree, Cluster, Cluster Perimeter, Lattice Animal, Percolation Threshold, Polyomino, s-Cluster, s-Run, Site Percolation
References
Deutscher, G.; Zallen, R.; and Adler, J. (Eds.). Percolation Structures and Processes. Bristol: Adam Hilger, 1983.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/rndprc/rndprc.html
Grimmett, G. Percolation. New York: Springer-Verlag, 1989.
Kesten, H. Percolation Theory for Mathematicians. Boston, MA: Birkhäuser, 1982.
Stauffer, D. and Aharony, A. Introduction to Percolation Theory, 2nd ed. London: Taylor & Francis, 1992.
Percolation Theory