|
|
|
Let ![]() be a number greater than 1,
be a number greater than 1, ![]() a Positive number, and
a Positive number, and
| (1) |
Pisot (1938) proved that if ![]() is such that there exists a
is such that there exists a ![]() such that the series
such that the series
![]() converges, then
converges, then ![]() is an Algebraic Integer whose conjugates all (except for itself)
have modulus
is an Algebraic Integer whose conjugates all (except for itself)
have modulus ![]() , and
, and ![]() is an algebraic Integer of the Field
is an algebraic Integer of the Field ![]() . Vijayaraghavan (1940) proved
that the set of Pisot-Vijayaraghavan numbers has infinitely many limit points. Salem (1944) proved that the set of
Pisot-Vijayaraghavan constants is closed. The proof of this theorem is based on the Lemma that for a
Pisot-Vijayaraghavan constant
. Vijayaraghavan (1940) proved
that the set of Pisot-Vijayaraghavan numbers has infinitely many limit points. Salem (1944) proved that the set of
Pisot-Vijayaraghavan constants is closed. The proof of this theorem is based on the Lemma that for a
Pisot-Vijayaraghavan constant ![]() , there always exists a number
, there always exists a number ![]() such that
such that
![]() and the
following inequality is satisfied,
and the
following inequality is satisfied,
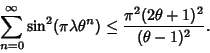 |
(2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| number | order | Polynomial | |
| 0 | 1.3247179572 | 3 | 1 0 |
| 1 | 1.3802775691 | 4 | 1 |
| 1.6216584885 | 16 | 1 |
|
| 1.8374664495 | 20 | 1 |
All the points in ![]() less than
less than ![]() are known (Dufresnoy and Pisot 1955). Each point of
are known (Dufresnoy and Pisot 1955). Each point of ![]() is a limit point
from both sides of the set
is a limit point
from both sides of the set ![]() of Salem Constants (Salem 1945).
of Salem Constants (Salem 1945).
See also Salem Constants
References
Boyd, D. W. ``Small Salem Numbers.'' Duke Math. J. 44, 315-328, 1977.
Dufresnoy, J. and Pisot, C. ``Étude de certaines fonctions méromorphes bornées sur le cercle unité,
application à un ensemble fermé d'entiers algébriques.'' Ann. Sci. École Norm. Sup. 72, 69-92, 1955.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 38 and 148, 1983.
Koksma, J. F. ``Ein mengentheoretischer Satz über die Gleichverteilung modulo Eins.'' Comp. Math. 2, 250-258, 1935.
Pisot, C. ``La répartition modulo 1 et les nombres algébriques.'' Annali di Pisa 7, 205-248, 1938.
Salem, R. ``Sets of Uniqueness and Sets of Multiplicity.'' Trans. Amer. Math. Soc. 54, 218-228, 1943.
Salem, R. ``A Remarkable Class of Algebraic Numbers. Proof of a Conjecture of Vijayaraghavan.'' Duke
Math. J. 11, 103-108, 1944.
Salem, R. ``Power Series with Integral Coefficients.'' Duke Math. J. 12, 153-172, 1945.
Siegel, C. L. ``Algebraic Numbers whose Conjugates Lie in the Unit Circle.'' Duke Math. J. 11, 597-602, 1944.
Vijayaraghavan, T. ``On the Fractional Parts of the Powers of a Number, II.'' Proc. Cambridge Phil. Soc. 37, 349-357, 1941.
|
|
|
© 1996-9 Eric W. Weisstein