Pólya Conjecture

Let $n$ be a Positive Integer and $r(n)$ the number of (not necessarily distinct) Prime Factors of $n$ (with $r(1)=0$). Let $O(m)$ be the number of Positive Integers $\leq m$ with an Odd number of Prime factors, and $E(m)$ the number of Positive Integers $\leq m$ with an Even number of Prime factors. Pólya conjectured that

$$L(m)\equiv E(m)-O(m)=\sum_{n=1}^m \lambda(n)$$

is $\leq 0$, where $\lambda(n)$ is the Liouville Function.

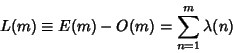
The conjecture was made in 1919, and disproven by Haselgrove (1958) using a method due to Ingham (1942). Lehman (1960) found the first explicit counterexample, $L(906{,}180{,}359)=1$, and the smallest counterexample $m=906{,}150{,}257$ was found by Tanaka (1980). The first $n$ for which $L(n)=0$ are $n=2$, 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (Tanaka 1980, Sloane's A028488). It is unknown if $L(x)$ changes sign infinitely often (Tanaka 1980).

See also Andrica's Conjecture, Liouville Function, Prime Factors

References

Haselgrove, C. B. ``A Disproof of a Conjecture of Pólya.'' Mathematika 5, 141-145, 1958.

Ingham, A. E. ``On Two Conjectures in the Theory of Numbers.'' Amer. J. Math. 64, 313-319, 1942.

Lehman, R. S. ``On Liouville's Function.'' Math. Comput. 14, 311-320, 1960.

Sloane, N. J. A. Sequence A028488 in ``The On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.

Tanaka, M. ``A Numerical Investigation on Cumulative Sum of the Liouville Function'' [sic]. Tokyo J. Math. 3, 187-189, 1980.