|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let ![]() be the probability that a Random Walk on a
be the probability that a Random Walk on a ![]() -D lattice returns to the origin. Pólya (1921) proved
that
-D lattice returns to the origin. Pólya (1921) proved
that
| (1) |
| (2) |
| (3) |
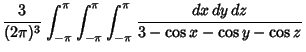 |
(4) | ||
| (5) | |||
![$\displaystyle 3(18+12\sqrt{2}-10\sqrt{3}-7\sqrt{6}\,)\left[{1+2\sum_{k=1}^\infty \mathop{\rm exp}\nolimits (-k^2\pi\sqrt{6}\,)}\right]^4$](p2_1191.gif) |
(6) | ||
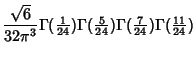 |
(7) | ||
| (8) |
| (9) |
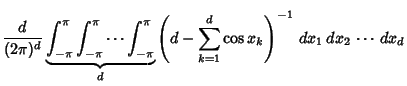 |
|||
![$\displaystyle \int_0^\infty \left[{I_0\left({t\over d}\right)}\right]^d e^{-t}\,dt,$](p2_1199.gif) |
(10) |
| 4 | 0.20 |
| 5 | 0.136 |
| 6 | 0.105 |
| 7 | 0.0858 |
| 8 | 0.0729 |
See also Random Walk
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/polya/polya.html
Domb, C. ``On Multiple Returns in the Random-Walk Problem.'' Proc. Cambridge Philos. Soc. 50, 586-591, 1954.
Glasser, M. L. and Zucker, I. J. ``Extended Watson Integrals for the Cubic Lattices.'' Proc. Nat. Acad. Sci. U.S.A. 74,
1800-1801, 1977.
McCrea, W. H. and Whipple, F. J. W. ``Random Paths in Two and Three Dimensions.'' Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.
Montroll, E. W. ``Random Walks in Multidimensional Spaces, Especially on Periodic Lattices.'' J. SIAM 4, 241-260, 1956.
Watson, G. N. ``Three Triple Integrals.'' Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.
|
|
|
© 1996-9 Eric W. Weisstein