Prime Quadruplet

A Prime Constellation of four successive Primes with minimal distance $(p,p+2,p+6,p+8)$. The quadruplet (2, 3, 5, 7) has smaller minimal distance, but it is an exceptional special case. With the exception of (5, 7, 11, 13), a prime quadruple must be of the form ($30n+11$, $30n+13$, $30n+17$, $30n+19$). The first few values of $n$ which give prime quadruples are $n=0$, 3, 6, 27, 49, 62, 69, 108, 115, ... (Sloane's A014561), and the first few values of $p$ are 5 (the exceptional case), 11, 101, 191, 821, 1481, 1871, 2081, 3251, 3461, .... The asymptotic Formula for the frequency of prime quadruples is analogous to that for other Prime Constellations,

$$P_x(p,p+2,p+6,p+8) \sim {27\over 2} \prod_{p\geq 5} {p^3(p-4)\over (p-1)^4} \int_2^x {dx\over (\ln x)^4}$$

$$= 4.151180864\int_2^x {dx\over (\ln x)^4},$$

where $c=4.15118\ldots$ is the Hardy-Littlewood constant for prime quadruplets. Roonguthai found the large prime quadruplets with

$$p = 10^{99}+349781731$$

$$p = 10^{199}+21156403891$$

$$p = 10^{299}+140159459341$$

$$p = 10^{399}+34993836001$$

$$p = 10^{499}+883750143961$$

$$p = 10^{599}+1394283756151$$

$$p = 10^{699}+547634621251$$

(Roonguthai).

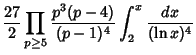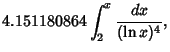See also Prime Arithmetic Progression, Prime Constellation, Prime k-Tuples Conjecture, Sexy Primes, Twin Primes

References

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. New York: Oxford University Press, 1979.

Forbes, T. ``Prime $k$-tuplets.'' http://www.ltkz.demon.co.uk/ktuplets.htm.

Rademacher, H. Lectures on Elementary Number Theory. New York: Blaisdell, 1964.

Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 61-62, 1994.

Roonguthai, W. ``Large Prime Quadruplets.'' http://www.mathsoft.com/asolve/constant/hrdyltl/roonguth.html.

Sloane, N. J. A. Sequence A014561 in ``The On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.