|
|
|
A primitive root of a Prime ![]() is an Integer
is an Integer ![]() satisfying
satisfying
![]() such that the residue classes of
such that the residue classes of ![]() ,
,
![]() ,
, ![]() , ...,
, ..., ![]() are all distinct, i.e.,
are all distinct, i.e., ![]() (mod
(mod ![]() ) has Order
) has Order ![]() (Ribenboim
1996, p. 22). If
(Ribenboim
1996, p. 22). If ![]() is a Prime Number, then there are exactly
is a Prime Number, then there are exactly ![]() incongruent primitive roots of
incongruent primitive roots of ![]() (Burton 1989,
p. 194).
(Burton 1989,
p. 194).
More generally, if ![]() (
(![]() and
and ![]() are Relatively Prime) and
are Relatively Prime) and ![]() is of Order
is of Order ![]() modulo
modulo ![]() , where
, where ![]() is the Totient Function, then
is the Totient Function, then ![]() is a primitive root of
is a primitive root of ![]() (Burton 1989, p. 187). In other
words,
(Burton 1989, p. 187). In other
words, ![]() has
has ![]() as a primitive root if
as a primitive root if
![]() , but
, but
![]() (mod
(mod ![]() ) for all positive integers
) for all positive integers
![]() . A primitive root of a number
. A primitive root of a number ![]() (but not necessarily
the smallest primitive root for composite
(but not necessarily
the smallest primitive root for composite ![]() ) can be computed using the Mathematica
) can be computed using the Mathematica
![]() routine NumberTheory`NumberTheoryFunctions`PrimitiveRoot[n].
routine NumberTheory`NumberTheoryFunctions`PrimitiveRoot[n].
If ![]() has a primitive root, then it has exactly
has a primitive root, then it has exactly ![]() of them (Burton 1989, p. 188). For
of them (Burton 1989, p. 188). For ![]() , 2, ..., the
first few values of
, 2, ..., the
first few values of ![]() are 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, 4, 8, ... (Sloane's A010554).
are 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, 4, 8, ... (Sloane's A010554). ![]() has a
primitive root if it is of the form 2, 4, a power
has a
primitive root if it is of the form 2, 4, a power ![]() , or twice a power
, or twice a power ![]() , where
, where ![]() is an Odd Prime and
is an Odd Prime and ![]() (Burton 1989, p. 204). The first few
(Burton 1989, p. 204). The first few ![]() for which primitive roots exist are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19,
22, ... (Sloane's A033948), so the number of primitive root of order
for which primitive roots exist are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19,
22, ... (Sloane's A033948), so the number of primitive root of order ![]() for
for ![]() , 2, ... are 0, 1, 1, 1, 2, 1, 2, 0, 2, 2,
4, 0, 4, (Sloane's A046144).
, 2, ... are 0, 1, 1, 1, 2, 1, 2, 0, 2, 2,
4, 0, 4, (Sloane's A046144).
The smallest primitive roots for the first few Integers ![]() are given in the following table (Sloane's A046145),
which omits
are given in the following table (Sloane's A046145),
which omits ![]() when
when ![]() does not exist.
does not exist.
| 2 | 1 | 38 | 3 | 94 | 5 | 158 | 3 |
| 3 | 2 | 41 | 6 | 97 | 5 | 162 | 5 |
| 4 | 3 | 43 | 3 | 98 | 3 | 163 | 2 |
| 5 | 2 | 46 | 5 | 101 | 2 | 166 | 5 |
| 6 | 5 | 47 | 5 | 103 | 5 | 167 | 5 |
| 7 | 3 | 49 | 3 | 106 | 3 | 169 | 2 |
| 9 | 2 | 50 | 3 | 107 | 2 | 173 | 2 |
| 10 | 3 | 53 | 2 | 109 | 6 | 178 | 3 |
| 11 | 2 | 54 | 5 | 113 | 3 | 179 | 2 |
| 13 | 2 | 58 | 3 | 118 | 11 | 181 | 2 |
| 14 | 3 | 59 | 2 | 121 | 2 | 191 | 19 |
| 17 | 3 | 61 | 2 | 122 | 7 | 193 | 5 |
| 18 | 5 | 62 | 3 | 125 | 2 | 194 | 5 |
| 19 | 2 | 67 | 2 | 127 | 3 | 197 | 2 |
| 22 | 7 | 71 | 7 | 131 | 2 | 199 | 3 |
| 23 | 5 | 73 | 5 | 134 | 7 | 202 | 3 |
| 25 | 2 | 74 | 5 | 137 | 3 | 206 | 5 |
| 26 | 7 | 79 | 3 | 139 | 2 | 211 | 2 |
| 27 | 2 | 81 | 2 | 142 | 7 | 214 | 5 |
| 29 | 2 | 82 | 7 | 146 | 5 | 218 | 11 |
| 31 | 3 | 83 | 2 | 149 | 2 | 223 | 3 |
| 34 | 3 | 86 | 3 | 151 | 6 | 226 | 3 |
| 37 | 2 | 89 | 3 | 157 | 5 | 227 | 2 |
Let ![]() be
any Odd Prime
be
any Odd Prime ![]() , and let
, and let
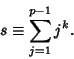 |
(1) |
| (2) |
| (3) |
| (4) |
| (5) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Primitive Roots.'' §24.3.4 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 827, 1972.
Burgess, D. A. ``On Character Sums and
Sloane, N. J. A. Sequences
A046145 and
A001918/M0242
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() -Series.'' Proc. London Math. Soc. 12, 193-206, 1962.Guy, R. K. ``Primitive Roots.'' §F9 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 248-249, 1994.
-Series.'' Proc. London Math. Soc. 12, 193-206, 1962.Guy, R. K. ``Primitive Roots.'' §F9 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 248-249, 1994.
|
|
|
© 1996-9 Eric W. Weisstein