|
|
|
A general plane quartic curve is a curve of the form
|
|
|
|
|
|
|
|
(1) |
The maximum number of Double Points for a nondegenerate quartic curve is three.
A quartic curve of the form
| (2) |
| (3) |
| (4) | |||
| (5) |
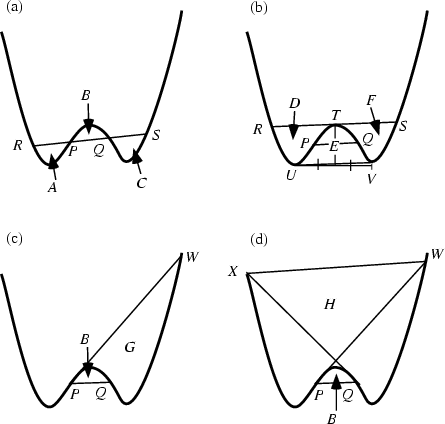
Let ![]() and
and ![]() be the Inflection Points and
be the Inflection Points and ![]() and
and ![]() the intersections of the line
the intersections of the line ![]() with the curve in Figure (a) above. Then
with the curve in Figure (a) above. Then
| (6) | |||
| (7) |
| (8) | |||
| (9) |
| (10) |
| (11) |
See also Cubic Surface, Pear-Shaped Curve, Solomon's Seal Lines
References
Coxeter, H. S. M. ``The Pure Archimedean Polytopes in Six and Seven Dimensions.''
Proc. Cambridge Phil. Soc. 24, 7-9, 1928.
Du Val, P. ``On the Directrices of a Set of Points in a Plane.'' Proc. London Math. Soc. Ser. 2 35, 23-74, 1933.
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 114-118, 1991.
Schoutte, P. H. ``On the Relation Between the Vertices of a Definite Sixdimensional Polytope and the Lines of a
Cubic Surface.'' Proc. Roy. Akad. Acad. Amsterdam 13, 375-383, 1910.
|
|
|
© 1996-9 Eric W. Weisstein