|
|
|
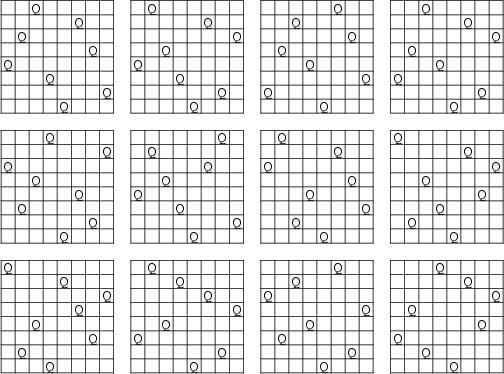
What is the maximum number of queens which can be placed on an ![]() Chessboard such that no two attack one
another? The answer is
Chessboard such that no two attack one
another? The answer is ![]() queens, which gives eight queens for the usual
queens, which gives eight queens for the usual ![]() board (Madachy 1979). The number
of different ways the
board (Madachy 1979). The number
of different ways the ![]() queens can be placed on an
queens can be placed on an ![]() chessboard so that no two queens may attack each other for
the first few
chessboard so that no two queens may attack each other for
the first few ![]() are 1, 0, 0, 2, 10, 4, 40, 92, ... (Sloane's A000170, Madachy 1979). The number of rotationally and
reflectively distinct solutions are 1, 0, 0, 1, 2, 1, 6, 12, 46, 92, ... (Sloane's A002562; Dudeney 1970; p. 96). The 12
distinct solutions for
are 1, 0, 0, 2, 10, 4, 40, 92, ... (Sloane's A000170, Madachy 1979). The number of rotationally and
reflectively distinct solutions are 1, 0, 0, 1, 2, 1, 6, 12, 46, 92, ... (Sloane's A002562; Dudeney 1970; p. 96). The 12
distinct solutions for ![]() are illustrated above, and the remaining 80 are generated by Rotation and
Reflection (Madachy 1979).
are illustrated above, and the remaining 80 are generated by Rotation and
Reflection (Madachy 1979).
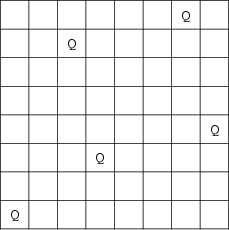
The minimum number of queens needed to occupy or attack all squares of an ![]() board is 5. Dudeney (1970, pp. 95-96)
gave the following results for the number of distinct arrangements
board is 5. Dudeney (1970, pp. 95-96)
gave the following results for the number of distinct arrangements ![]() of
of ![]() queens attacking or occupying every
square of an
queens attacking or occupying every
square of an ![]() board for which every queen is attacked (``protected'') by at least one other.
board for which every queen is attacked (``protected'') by at least one other.
| 2 | 4 | 3 |
| 3 | 5 | 37 |
| 3 | 6 | 1 |
| 4 | 7 | 5 |
Dudeney (1970, pp. 95-96) also gave the following results for the number of distinct arrangements ![]() of
of ![]() queens
attacking or occupying every square of an
queens
attacking or occupying every square of an ![]() board for which no two queens attack one another (they are ``not
protected'').
board for which no two queens attack one another (they are ``not
protected'').
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 3 | 4 | 2 |
| 3 | 5 | 2 |
| 4 | 6 | 17 |
| 4 | 7 | 1 |
| 5 | 8 | 91 |
Vardi (1991) generalizes the problem from a square chessboard to one with the topology of the Torus. The number of
solutions for ![]() queens with
queens with ![]() Odd are 1, 0, 10, 28, 0, 88, ... (Sloane's A007705). Vardi (1991) also considers the
toroidal ``semiqueens'' problem, in which a semiqueen can move like a rook or bishop, but only on Positive broken
diagonals. The number of solutions to this problem for
Odd are 1, 0, 10, 28, 0, 88, ... (Sloane's A007705). Vardi (1991) also considers the
toroidal ``semiqueens'' problem, in which a semiqueen can move like a rook or bishop, but only on Positive broken
diagonals. The number of solutions to this problem for ![]() queens with
queens with ![]() Odd are 1, 3, 15, 133, 2025, 37851, ...
(Sloane's A006717), and 0 for Even
Odd are 1, 3, 15, 133, 2025, 37851, ...
(Sloane's A006717), and 0 for Even ![]() .
.
Chow and Velucchi give the solution to the question, ``How many different arrangements of ![]() queens are possible on an
order
queens are possible on an
order ![]() chessboard?'' as 1/8th of the Coefficient of
chessboard?'' as 1/8th of the Coefficient of ![]() in the Polynomial
in the Polynomial
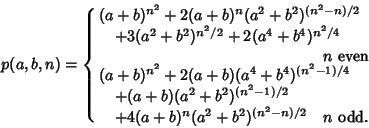
See also Bishops Problem, Chess, Kings Problem, Knights Problem, Knight's Tour, Rooks Problem
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 166-169, 1987.
Campbell, P. J. ``Gauss and the 8-Queens Problem: A Study in the Propagation of Historical Error.'' Historia Math. 4, 397-404, 1977.
Chow, T. and Velucchi, M. ``Different Dispositions in the Chessboard.''
http://www.cli.di.unipi.it/~velucchi/diff.txt.
Dudeney, H. E. ``The Eight Queens.'' §300 in Amusements in Mathematics. New York: Dover, p. 89, 1970.
Erbas, C. and Tanik, M. M. ``Generating Solutions to the
Erbas, C.; Tanik, M. M.; and Aliyzaicioglu, Z. ``Linear Congruence Equations for the Solutions of the
Ginsburg, J. ``Gauss's Arithmetization of the Problem of
Guy, R. K. ``The
Kraitchik, M. ``The Problem of the Queens'' and ``Domination of the Chessboard.'' §10.3 and 10.4
in Mathematical Recreations. New York: W. W. Norton, pp. 247-256, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 34-36, 1979.
Pólya, G. ``Über die `doppelt-periodischen' Lösungen des
Riven, I.; Vardi, I.; and Zimmerman, P. ``The
Riven, I. and Zabih, R. ``An Algebraic Approach to Constraint Satisfaction Problems.'' In
Proc. Eleventh Internat. Joint Conference on Artificial Intelligence, Vol. 1, August 20-25, 1989.
Detroit, MI: IJCAII, pp. 284-289, 1989.
Ruskey, F. ``Information on the
Sloane, N. J. A. Sequences
A001366,
A000170/M1958,
A006717/M3005,
A007705/M4691,
A002562/M0180
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Vardi, I. ``The
Velucchi, M. ``Non-Dominating Queens Problem.''
http://www.cli.di.unipi.it/~velucchi/queens.txt.
![]() -Queens Problem Using 2-Circulants.''
Math. Mag. 68, 343-356, 1995.
-Queens Problem Using 2-Circulants.''
Math. Mag. 68, 343-356, 1995.
![]() -Queens
Problem.'' Inform. Proc. Let. 41, 301-306, 1992.
-Queens
Problem.'' Inform. Proc. Let. 41, 301-306, 1992.
![]() Queens.'' Scripta Math. 5, 63-66, 1939.
Queens.'' Scripta Math. 5, 63-66, 1939.
![]() Queens Problem.'' §C18 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.
Queens Problem.'' §C18 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.
![]() -Damen-Problems.'' In Mathematische Unterhaltungen und Spiele
(Ed. W. Ahrens). 1918.
-Damen-Problems.'' In Mathematische Unterhaltungen und Spiele
(Ed. W. Ahrens). 1918.
![]() -Queens Problem.'' Amer. Math. Monthly 101, 629-639, 1994.
-Queens Problem.'' Amer. Math. Monthly 101, 629-639, 1994.
![]() Queens Problem.''
http://sue.csc.uvic.ca/~cos/inf/misc/Queen.html.
Queens Problem.''
http://sue.csc.uvic.ca/~cos/inf/misc/Queen.html.
![]() -Queens Problems.'' Ch. 6 in Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, pp. 107-125, 1991.
-Queens Problems.'' Ch. 6 in Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, pp. 107-125, 1991.
|
|
|
© 1996-9 Eric W. Weisstein