|
|
|
Let ![]() be a discriminant,
be a discriminant,
| (1) |
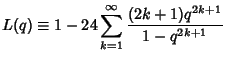 |
|||
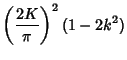 |
(2) | ||
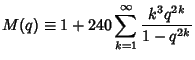 |
|||
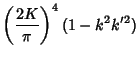 |
(3) | ||
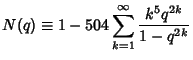 |
|||
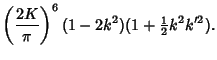 |
(4) |
See also Klein's Absolute Invariant, Pi
References
Borwein, J. M. and Borwein, P. B. ``Class Number Three Ramanujan Type Series for
Ramanujan, S. ``Modular Equations and Approximations to
![]() .''
J. Comput. Appl. Math. 46, 281-290, 1993.
.''
J. Comput. Appl. Math. 46, 281-290, 1993.
![]() .'' Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.