|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Given the Closed Interval ![]() with
with ![]() , let 1-D ``cars'' of unit length be parked randomly on the interval.
The Mean number
, let 1-D ``cars'' of unit length be parked randomly on the interval.
The Mean number ![]() of cars which can fit (without overlapping!) satisfies
of cars which can fit (without overlapping!) satisfies
| (1) |
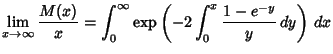 |
|||
| (2) |
| (3) |
![\begin{displaymath}
M(x)=mx+m-1+{\mathcal O}\left[{\left({2e\over x}\right)^{x-3/2}}\right].
\end{displaymath}](r_1214.gif) |
(4) |
| (5) |
Let ![]() be the variance of the number of cars, then Dvoretzky and Robbins (1964) and
Mannion (1964) showed that
be the variance of the number of cars, then Dvoretzky and Robbins (1964) and
Mannion (1964) showed that
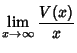 |
|||
![$\displaystyle 2\int_0^\infty \left\{{x\int_0^1 e^{-xy}R_2(y)\,dy+x^2\left[{\int_0^\infty e^{-xy}R_1(y)\,dy}\right]^2}\right\}$](r_1219.gif) |
|||
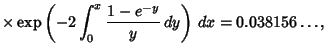 |
(6) |
where
| (7) | |||
![$\displaystyle \left\{\begin{array}{ll} (1-m-mx)^2 & \mbox{for $0\leq x\leq 1$}\...
...+ \int_0^{x-1} R_1(y)R_1(x-y-1)\,dy}\right]& \mbox{for $x>1$}\end{array}\right.$](r_1224.gif) |
(8) |
| (9) |
![\begin{displaymath}
V(x)=vx+v+{\mathcal O}\left[{\left({4e\over x}\right)^{x-4}}\right].
\end{displaymath}](r_1226.gif) |
(10) |
Palasti (1960) conjectured that in 2-D,
| (11) |
References
Blaisdell, B. E. and Solomon, H. ``On Random Sequential Packing in the Plane and a Conjecture of Palasti.''
J. Appl. Prob. 7, 667-698, 1970.
Dvoretzky, A. and Robbins, H. ``On the Parking Problem.'' Publ. Math. Inst. Hung. Acad. Sci. 9, 209-224, 1964.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/renyi/renyi.html
Mannion, D. ``Random Space-Filling in One Dimension.'' Publ. Math. Inst. Hung. Acad. Sci. 9, 143-154, 1964.
Palasti, I. ``On Some Random Space Filling Problems.'' Publ. Math. Inst. Hung. Acad. Sci. 5, 353-359, 1960.
Rényi, A. ``On a One-Dimensional Problem Concerning Random Space-Filling.''
Publ. Math. Inst. Hung. Acad. Sci. 3, 109-127, 1958.
Solomon, H. and Weiner, H. J. ``A Review of the Packing Problem.'' Comm. Statist. Th. Meth. 15, 2571-2607, 1986.
|
|
|
© 1996-9 Eric W. Weisstein