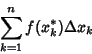Let a Closed Interval ![$[a,b]$](r_1455.gif) be partitioned by points
be partitioned by points
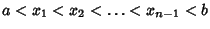 , the lengths of the resulting
intervals between the points are denoted
, the lengths of the resulting
intervals between the points are denoted 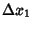 ,
, 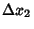 , ...,
, ..., 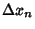 . Then the quantity
. Then the quantity
is called a Riemann sum for a given function 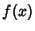 and partition. The value
and partition. The value
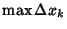 is
called the Mesh Size of the partition. If the Limit
is
called the Mesh Size of the partition. If the Limit
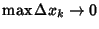 exists, this limit is known
as the Riemann Integral of
exists, this limit is known
as the Riemann Integral of 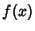 over the interval
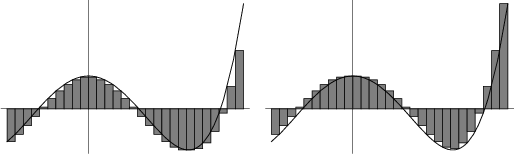
over the interval ![$[a,b]$](r_1455.gif) . The shaded areas in the above plots show the
Lower and Upper Sums for a constant Mesh Size.
. The shaded areas in the above plots show the
Lower and Upper Sums for a constant Mesh Size.
See also Lower Sum, Riemann Integral, Upper Sum
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be partitioned by points
be partitioned by points
![]() , the lengths of the resulting
intervals between the points are denoted
, the lengths of the resulting
intervals between the points are denoted ![]() ,
, ![]() , ...,
, ..., ![]() . Then the quantity
. Then the quantity