Roman Surface

A Quartic Nonorientable Surface, also known as the Steiner Surface. The Roman surface is one of the three possible surfaces obtained by sewing a Möbius Strip to the edge of a Disk. The other two are the Boy Surface and Cross-Cap, all of which are homeomorphic to the Real Projective Plane (Pinkall 1986).

The center point of the Roman surface is an ordinary Triple Point with $(\pm 1, 0, 0) = (0, \pm 1, 0) = (0, 0, \pm 1)$, and the six endpoints of the three lines of self-intersection are singular Pinch Points, also known as Whitney Singularities. The Roman surface is essentially six Cross-Caps stuck together and contains a double Infinity of Conics.

The Roman surface can given by the equation

$$(x^2+y^2+z^2-k^2)^2=[(z-k)^2-2x^2][(z+k)^2-2y^2].$$ (1)

Solving for $z$ gives the pair of equations

$$z={k(y^2-x^2)\pm(x^2-y^2)\sqrt{k^2-x^2-y^2}\over 2(x^2+y^2)}.$$ (2)

If the surface is rotated by 45° about the z-Axis via the Rotation Matrix

$${\hbox{\sf R}}_z(45^\circ)={1\over\sqrt{2}}\left[{\matrix{1 & 1 & 0\cr -1 & 1 & 0\cr 0 & 0 & 1\cr}}\right]$$ (3)

to give

$$\left[{\matrix{x'\cr y'\cr z'\cr}}\right] = {\hbox{\sf R}}_z(45^\circ)\left[{\matrix{x\cr y\cr z\cr}}\right],$$ (4)

then the simple equation

$$x^2y^2+x^2z^2+y^2z^2+2kxyz=0$$ (5)

results. The Roman surface can also be generated using the general method for Nonorientable Surfaces using the polynomial function

$${\bf f}(x,y,z)=(xy, yz, zx)$$ (6)

(Pinkall 1986). Setting

$$x = \cos u\sin v$$ (7)

$$y = \sin u\sin v$$ (8)

$$z = \cos v$$ (9)

in the former gives

$$x(u,v) = {\textstyle{1\over 2}}\sin(2u)\sin^2v$$ (10)

$$y(u,v) = {\textstyle{1\over 2}}\sin u\cos(2v)$$ (11)

$$z(u,v) = {\textstyle{1\over 2}}\cos u\sin(2v)$$ (12)

for $u\in[0,2\pi)$ and $v\in[-\pi/2,\pi/2]$. Flipping $\sin v$ and $\cos v$ and multiplying by 2 gives the form shown by Wang.

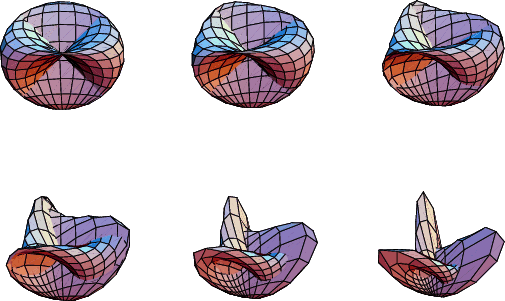
A Homotopy (smooth deformation) between the Roman surface and Boy Surface is given by the equations

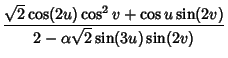$$x(u,v) = {\sqrt{2}\cos(2u)\cos^2v+\cos u\sin(2v)\over 2-\alpha\sqrt{2}\sin(3u)\sin(2v)}$$ (13)

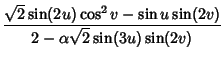$$y(u,v) = {\sqrt{2}\sin(2u)\cos^2v-\sin u\sin(2v)\over 2-\alpha\sqrt{2}\sin(3u)\sin(2v)}$$ (14)

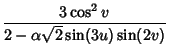$$z(u,v) = {3\cos^2v\over 2-\alpha\sqrt{2}\sin(3u)\sin(2v)}$$ (15)

for $u\in[-\pi/2,\pi/2]$ and $v\in[0,\pi]$ as $\alpha$ varies from 0 to 1. $\alpha=0$ corresponds to the Roman surface and $\alpha=1$ to the Boy Surface (Wang).

See also Boy Surface, Cross-Cap, Heptahedron, Möbius Strip, Nonorientable Surface, Quartic Surface, Steiner Surface

References

Fischer, G. (Ed.). Mathematical Models from the Collections of Universities and Museums. Braunschweig, Germany: Vieweg, p. 19, 1986.

Fischer, G. (Ed.). Plates 42-44 and 108-114 in Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, pp. 42-44 and 108-109, 1986.

Geometry Center. ``The Roman Surface.'' http://www.geom.umn.edu/zoo/toptype/pplane/roman/.

Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 242-243, 1993.

Nordstrand, T. ``Steiner's Roman Surface.'' http://www.uib.no/people/nfytn/steintxt.htm.

Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, p. 64, 1986.

Wang, P. ``Renderings.'' http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/.