|
|
|

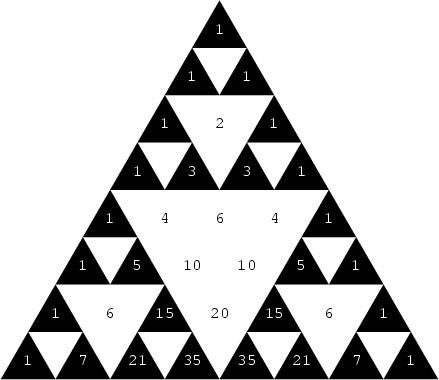
A Fractal described by Sierpinski in 1915. It is also called the Sierpinski Gasket or Sierpinski Triangle. The curve can be written as a Lindenmayer System with initial string "FXF-FF-FF", String Rewriting rules "F" -> "FF", "X" -> "-FXF++FXF++FXF-", and angle 60°.
Let ![]() be the number of black triangles after iteration
be the number of black triangles after iteration
![]() ,
, ![]() the length of a side of a triangle, and
the length of a side of a triangle, and ![]() the fractional Area which is black after the
the fractional Area which is black after the ![]() th
iteration. Then
th
iteration. Then
| (1) | |||
| (2) | |||
| (3) |
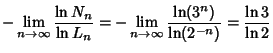 |
|||
| (4) |
See also Lindenmayer System, Sierpinski Arrowhead Curve, Sierpinski Carpet, Tetrix
References
Crownover, R. M. Introduction to Fractals and Chaos. Sudbury, MA: Jones & Bartlett, 1995.
Dickau, R. M. ``Two-Dimensional L-Systems.''
http://forum.swarthmore.edu/advanced/robertd/lsys2d.html.
Dickau, R. M. ``Typeset Fractals.'' Mathematica J. 7, 15, 1997.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press,
pp. 13-14, 1991.
Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science.
New York: Springer-Verlag, pp. 78-88, 1992.
Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, p. 282, 1988.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 108 and 151-153, 1991.
Wang, P. ``Renderings.'' http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/.
![]() Dickau, R. ``Sierpinski-Menger Sponge Code and Graphic.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Graphics/0206-110.
Dickau, R. ``Sierpinski-Menger Sponge Code and Graphic.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Graphics/0206-110.
![]() Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.
Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.
|
|
|
© 1996-9 Eric W. Weisstein