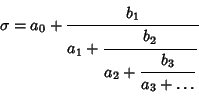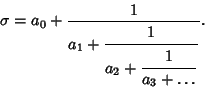Simple Continued Fraction

A Continued Fraction

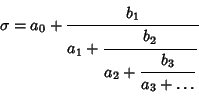$$\sigma=a_0+{\strut\displaystyle b_1\over{\strut\displaystyle... ...\strut\displaystyle b_3\over\strut\displaystyle a_3+\ldots}}}}$$ (1)

in which the 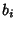$b_i$s are all unity, leaving a continued fraction of the form

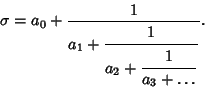$$\sigma = a_0+{1\over{\strut\displaystyle a_1+{\strut\display... ...{\strut\displaystyle 1\over\strut\displaystyle a_3+\ldots}}}}.$$ (2)

A simple continued fraction can be written in a compact abbreviated Notation as

$$\sigma=[a_0, a_1, a_2, a_3, \ldots].$$ (3)

Bach and Shallit (1996) show how to compute the Jacobi Symbol in terms of the simple continued fraction of a Rational Number 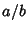$a/b$.

See also Continued Fraction

References

Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, pp. 343-344, 1996.