The degree of asymmetry of a distribution. If the distribution has a longer tail less than the maximum, the function has
Negative skewness. Otherwise, it has Positive skewness. Several types of skewness are defined. The
Fisher Skewness is defined by
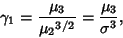 |
(1) |
where 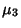 is the third Moment, and
is the third Moment, and
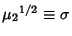 is the Standard Deviation. The
Pearson Skewness is defined by
is the Standard Deviation. The
Pearson Skewness is defined by
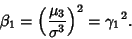 |
(2) |
The Momental Skewness is defined by
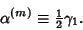 |
(3) |
The Pearson Mode Skewness is defined by
![\begin{displaymath}
{[{\rm mean}]-[{\rm mode}]\over \sigma}.
\end{displaymath}](s2_26.gif) |
(4) |
Pearson's Skewness Coefficients are defined by
![\begin{displaymath}
{3[{\rm mean}]-[{\rm mode}]\over s}
\end{displaymath}](s2_27.gif) |
(5) |
and
![\begin{displaymath}
{3[{\rm mean}]-[{\rm median}]\over s}.
\end{displaymath}](s2_28.gif) |
(6) |
The Bowley Skewness (also known as Quartile Skewness Coefficient) is defined by
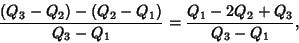 |
(7) |
where the 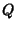 s denote the Interquartile Ranges.
The Momental Skewness is
s denote the Interquartile Ranges.
The Momental Skewness is
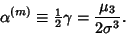 |
(8) |
An Estimator for the Fisher Skewness 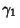 is
is
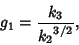 |
(9) |
where the 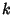 s are k-Statistic. The Standard Deviation of
s are k-Statistic. The Standard Deviation of 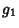 is
is
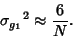 |
(10) |
See also Bowley Skewness, Fisher Skewness,
Gamma Statistic, Kurtosis, Mean, Momental Skewness,
Pearson Skewness, Standard Deviation
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 928, 1972.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Moments of a Distribution: Mean,
Variance, Skewness, and So Forth.'' §14.1 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 604-609, 1992.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is
is