Snub Cube

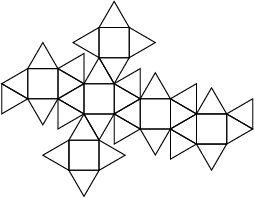
$\begin{figure}\begin{figure}\begin{center}\BoxedEPSF{Snub_Cube_net.epsf scaled 600}\end{center}\end{figure}\par\end{figure}$

An Archimedean Solid also called the Snub Cuboctahedron whose Vertices are the 24 points on the surface of a Sphere for which the smallest distance between any two is as great as possible. It has two Enantiomers, and its Dual Polyhedron is the Pentagonal Icositetrahedron. It has Schläfli Symbol s $\left\{{3\atop 4}\right\}$ . It is also Uniform Polyhedron $U_{12}$ and has Wythoff Symbol $\vert\,2\,3\,4$ . Its faces are $32\{3\}+6\{4\}$ .

$\displaystyle r$	$\textstyle =$	$\displaystyle 1.157661791\ldots$
$\displaystyle \rho$	$\textstyle =$	$\displaystyle 1.247223168\ldots$
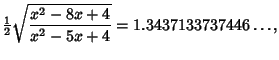$\displaystyle R$	$\textstyle =$	$\displaystyle {\textstyle{1\over 2}}\sqrt{x^2-8x+4\over x^2-5x+4}=1.3437133737446\ldots,$

where

$\begin{displaymath} x\equiv (19+3\sqrt{33}\,)^{1/3}, \end{displaymath}$

and the exact expressions for

and $\rho$ can be computed using

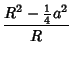$\displaystyle r$	$\textstyle =$	$\displaystyle {R^2-{\textstyle{1\over 4}}a^2\over R}$
$\displaystyle \rho$	$\textstyle =$	$\displaystyle \sqrt{R^2-{\textstyle{1\over 4}}a^2}.$

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 139, 1987.

Coxeter, H. S. M.; Longuet-Higgins, M. S.; and Miller, J. C. P. ``Uniform Polyhedra.'' Phil. Trans. Roy. Soc. London Ser. A 246, 401-450, 1954.