|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Expanding the Riemann Zeta Function about ![]() gives
gives
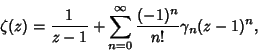 |
(1) |
![\begin{displaymath}
\gamma_n\equiv\lim_{m\to\infty}\left[{\,\sum_{k=1}^m {(\ln k)^n\over k}-{(\ln m)^{n+1}\over n+1}}\right].
\end{displaymath}](s3_850.gif) |
(2) |
| (3) |
| 0 | 0.5772156649 |
| 1 |
|
| 2 |
|
| 3 | 0.002053834420 |
| 4 | 0.002325370065 |
| 5 | 0.0007933238173 |
Briggs (1955-1956) proved that there infinitely many ![]() of each Sign. Berndt (1972) gave upper bounds of
of each Sign. Berndt (1972) gave upper bounds of
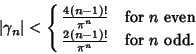 |
(4) |
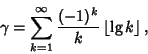 |
(5) |
![\begin{displaymath}
{2\gamma_1\over\ln 2}=\sum_{k=1}^\infty {(-1)^k\over k}[2\lg...
...oor{\lg (2k)}\right\rfloor ]\left\lfloor{\lg k}\right\rfloor .
\end{displaymath}](s3_859.gif) |
(6) |
A set of constants related to ![]() is
is
![\begin{displaymath}
\delta_n\equiv\lim_{m\to\infty}\left[{\sum_{k=1}^m (\ln k)^n-\int_1^m (\ln x)^n\,dx-{\textstyle{1\over 2}}(\ln m)^n}\right]
\end{displaymath}](s3_861.gif) |
(7) |
References
Berndt, B. C. ``On the Hurwitz Zeta-Function.'' Rocky Mountain J. Math. 2, 151-157, 1972.
Bohman, J. and Fröberg, C.-E. ``The Stieltjes Function--Definitions and Properties.'' Math. Comput.
51, 281-289, 1988.
Briggs, W. E. ``Some Constants Associated with the Riemann Zeta-Function.'' Mich. Math. J. 3, 117-121,
1955-1956.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/stltjs/stltjs.html
Hardy, G. H. ``Note on Dr. Vacca's Series for
Kluyver, J. C. ``On Certain Series of Mr. Hardy.'' Quart. J. Pure Appl. Math. 50, 185-192, 1927.
Knopfmacher, J. ``Generalised Euler Constants.'' Proc. Edinburgh Math. Soc. 21, 25-32, 1978.
Lehmer, D. H. ``The Sum of Like Powers of the Zeros of the Riemann Zeta Function.'' Math. Comput. 50,
265-273, 1988.
Liang, J. J. Y. and Todd, J. ``The Stieltjes Constants.'' J. Res. Nat. Bur. Standards--Math. Sci. 76B,
161-178, 1972.
Sitaramachandrarao, R. ``Maclaurin Coefficients of the Riemann Zeta Function.'' Abstracts Amer. Math. Soc.
7, 280, 1986.
Vacca, G. ``A New Series for the Eulerian Constant.'' Quart. J. Pure Appl. Math. 41, 363-368, 1910.
![]() .'' Quart. J. Pure Appl. Math. 43, 215-216,
1912.
.'' Quart. J. Pure Appl. Math. 43, 215-216,
1912.
|
|
|
© 1996-9 Eric W. Weisstein