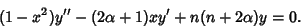Ultraspherical Differential Equation

$\begin{displaymath} (1-x^2) y''-(2\alpha+1)x y'+n(n+2\alpha)y = 0. \end{displaymath}$

(1)

Alternate forms are

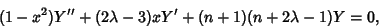$\begin{displaymath} (1-x^2)Y''+(2\lambda-3)xY'+(n+1)(n+2\lambda-1)Y=0, \end{displaymath}$

(2)

where

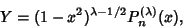$\begin{displaymath} Y=(1-x^2)^{\lambda-1/2}P_n^{(\lambda)}(x), \end{displaymath}$

(3)

$\begin{displaymath} {d^2u\over dx^2}+\left[{{(n+\lambda)^2\over 1-x^2}+{{\textst... ...lambda^2+{\textstyle{1\over 4}}x^2\over (1-x^2)^2}}\right]u=0, \end{displaymath}$

(4)

where

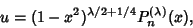$\begin{displaymath} u=(1-x^2)^{\lambda/2+1/4} P_n^{(\lambda)}(x), \end{displaymath}$

(5)

and

$\begin{displaymath} {d^2u\over d\theta^2}+\left[{(n+\lambda)^2+{\lambda(1-\lambda)\over\sin^2\theta}}\right]u=0, \end{displaymath}$

(6)

where

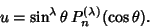$\begin{displaymath} u=\sin^\lambda\theta \,P_n^{(\lambda)}(\cos\theta). \end{displaymath}$

(7)

The solutions are the Ultraspherical Functions 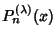$P_n^{(\lambda)}(x)$ . For integral

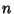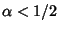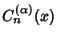with $\alpha < 1/2$ , the function converges to the Ultraspherical Polynomials $C_n^{(\alpha)}(x)$ .

References

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 547-549, 1953.